题目内容
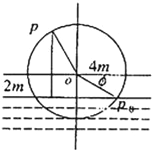
【题目】如图，一个水轮的半径为4m，水轮圆心O距离水面2m，已知水轮每分钟转动5圈，如果当水轮上点P从水中浮现时（图中点p0）开始计算时间．
（1）将点p距离水面的高度z（m）表示为时间t（s）的函数；
（2）点p第一次到达最高点大约需要多少时间？
【答案】（1）
（2）点P第一次到达最高点大约需要4s．
【解析】试题分析：（1）令函数为
，由题意可知函数最大值与最小值，由两最值可得振幅
与
，再由每分钟转过的角度可得周期，利用周期与
的关系可得其值，再将起始位置时， 
满足函数表达式代入可得
值；（2）当函数取最值时，求出对应的
值，取最小正值，即为所需要时间．
试题解析：（1）依题意可知z的最大值为6，最小为﹣2，
∴
；
∵op每秒钟内所转过的角为
，得z=4sin
，
当t=0时，z=0，得sinφ=﹣
，即φ=﹣
，故所求的函数关系式为
z=4sin
+2
（2）令z=4sin
+2=6，得sin=1，
取
，得t=4，
故点P第一次到达最高点大约需要4s．
练习册系列答案
相关题目
