题目内容
18.定义在[-1,1]上的函数y=f(x)是增函数,且是奇函数,若f(a-1)+f(4a-5)>0,求实数a的取值范围.分析 根据条件f(x)为奇函数,且在[-1,1]上为增函数,便可由f(a-1)+f(4a-5)>0得到f(a-1)>f(5-4a),进一步得到$\left\{\begin{array}{l}{-1≤a-1≤1}\\{-1≤5-4a≤1}\\{a-1>5-4a}\end{array}\right.$,这样解该不等式组便可得出实数a的取值范围.
解答 解:f(x)是定义在[-1,1]上的奇函数;
∴由f(a-1)+f(4a-5)>0得,f(a-1)>f(5-4a);
又f(x)在[-1,1]上为增函数;
∴$\left\{\begin{array}{l}{-1≤a-1≤1}\\{-1≤5-4a≤1}\\{a-1>5-4a}\end{array}\right.$;
解得$\frac{6}{5}<a≤\frac{3}{2}$;
∴实数a的取值范围是$(\frac{6}{5},\frac{3}{2}]$.
点评 考查奇函数的定义,增函数的定义,以及根据增函数的定义解不等式,注意要使a-1,5-4a在定义域[-1,1]内.

练习册系列答案
相关题目
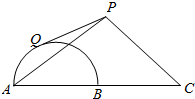 在如图所示的平面中,点C为半圆的直径AB延长线上的一点,AB=BC=2,过动点P作半圆的切线PQ,若PC=$\sqrt{2}$PQ,则△PAC的面积的最大值为4$\sqrt{5}$.
在如图所示的平面中,点C为半圆的直径AB延长线上的一点,AB=BC=2,过动点P作半圆的切线PQ,若PC=$\sqrt{2}$PQ,则△PAC的面积的最大值为4$\sqrt{5}$.