题目内容
在海南省第二十六届科技创新大赛活动中，某同学为研究“网络游戏对当代青少年的影响”作了一次调查，共调查了50名同学，其中男生26人，有8人不喜欢玩电脑游戏，而调查的女生中有9人喜欢玩电脑游戏．
（Ⅰ）根据以上数据建立一个2×2的列联表；
（Ⅱ）请画出上述列联表的等高条形图．
（Ⅰ）根据以上数据建立一个2×2的列联表；
性别 游戏态度 | 男生 | 女生 | 合计 |
| 喜欢玩电脑游戏 | |||
| 不喜欢玩电脑游戏 | |||
| 合计 | 50 |
考点：独立性检验的基本思想
专题：概率与统计
分析：（Ⅰ）根据所给的数据，分别计算出a，b，c，d的值，可画出列联表；
（Ⅱ）根据所给的数据，分别计算出男生，女生中喜欢玩电脑游戏的比例，可得等高条形图．
（Ⅱ）根据所给的数据，分别计算出男生，女生中喜欢玩电脑游戏的比例，可得等高条形图．
解答：解：（Ⅰ）2×2列联表
（Ⅱ）上述列联表的等高条形图如下所示：
| 性别 游戏态度 | 男生 | 女生 | 总计 |
| 喜欢玩电脑游戏 | 18 | 9 | 27 |
| 不喜欢玩电脑游戏 | 8 | 15 | 23 |
| 总计 | 26 | 24 | 50 |
点评：本题考查独立性检验的应用，解题的关键是根据已知求出表中各个单元格的数据．
练习册系列答案
相关题目
下列命题中真命题是（ ）
| A、相关系数r（|r|≤1），|r|值越小，变量之间的线性相关程度越高 | B、“存在x∈R，使得x2+x+1＜0”的否定是“对任意x∈R．均有x2+x+1＜0” | C、命题“在△ABC中，若A＞B，则sinA＞sinB”的逆命题为假命题 | D、“b=0”是“函数f（x）=ax2+bx+c是偶函数”的充要条件 |
已知直线y=k（x+1）与抛物线C：y2=4x相交于点A，B两点，F为抛物线C的焦点，若|FA|=3|FB|，则k=（ ）
A、±
| ||||
B、±
| ||||
C、±
| ||||
D、±
|
函数f（x）=-x3+3x2-4的单调递增区间是（ ）
| A、（-∞，0） | B、（-2，0） | C、（0，2） | D、（2，+∞） |
已知等差数列{an}中的两项a2，a2014是函数f（x）=
x3-3x2+ax（a为常数）的极值点，且a1008+a1009＜0，则使{an}的前n项和Sn取得最大值的n为（ ）
| 1 |
| 3 |
| A、1008 |
| B、1009 |
| C、1008，1009 |
| D、2014 |
设f为实系数三次多项式函数．已知五个方程式的相异实根个数如下表所述﹕
关于f的极小值α﹐试问下列选项是正确的﹖（ ）
| f（x）-20=0 | 1 | f（x）+10=0 | 1 |
| f（x）-10=0 | 3 | f（x）+20=0 | 1 |
| f（x）=0 | 3 |
| A、0＜α＜10 |
| B、-20＜α＜-10 |
| C、-10＜α＜0 |
| D、α不存在 |
复数
（i为虚数单位）在复平面上对应的点在（ ）
| 2+i |
| i3 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
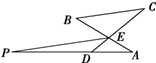如图，AB与CD相交于点E，过E作BC的平行线与AD的延长线交于点P，已知∠A=∠C，PD=2DA=2，求PE的长．