题目内容
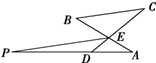如图，AB与CD相交于点E，过E作BC的平行线与AD的延长线交于点P，已知∠A=∠C，PD=2DA=2，求PE的长．考点：相似三角形的性质
专题：选作题,几何证明
分析：利用已知条件判断△EPD∽△APE，列出比例关系，即可求解PE的值．
解答：解：∵BC∥PE，∴∠BCD=∠PED，
在圆中∠BCD=∠BAD，∴∠PED=∠BAD，
∴△EPD∽△APE，
∴
=
∵PD=2DA=2
∴PE2=PA•PD=3×2=6，
∴PE=
．
在圆中∠BCD=∠BAD，∴∠PED=∠BAD，
∴△EPD∽△APE，
∴
| PE |
| PA |
| PD |
| PE |
∵PD=2DA=2
∴PE2=PA•PD=3×2=6，
∴PE=
| 6 |
点评：本题考查三角形相似的判断与性质定理的应用，考查计算能力．
练习册系列答案
相关题目
若平面α，β的法向量分别为
=（-1，2，4），
=（x，-1，-2），并且α∥β，则x的值为（ ）
| a |
| b |
| A、10 | ||
| B、-10 | ||
C、
| ||
D、-
|
（x2+
）6中x3的系数为（ ）
| 1 |
| x |
| A、20 | B、30 | C、25 | D、40 |