题目内容
已知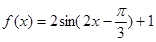 .
.
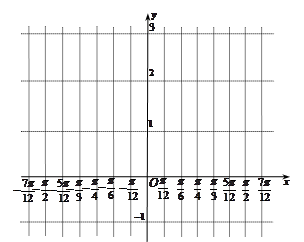
(1)求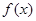 的单调增区间;
的单调增区间;
(2)求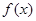 图象的对称轴的方程和对称中心的坐标;(3)在给出的直角坐标系中,请画出
图象的对称轴的方程和对称中心的坐标;(3)在给出的直角坐标系中,请画出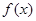 在区间[
在区间[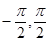 ]上的图象.
]上的图象.
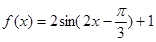 .
.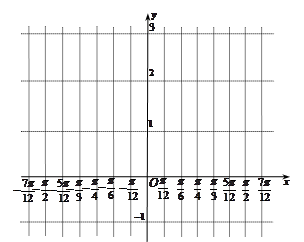
(1)求
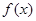 的单调增区间;
的单调增区间;(2)求
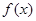 图象的对称轴的方程和对称中心的坐标;(3)在给出的直角坐标系中,请画出
图象的对称轴的方程和对称中心的坐标;(3)在给出的直角坐标系中,请画出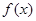 在区间[
在区间[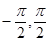 ]上的图象.
]上的图象.(1) ;(2)对称轴方程
;(2)对称轴方程 ,对称中心
,对称中心 ;(3)详见解析.
;(3)详见解析.
 ;(2)对称轴方程
;(2)对称轴方程 ,对称中心
,对称中心 ;(3)详见解析.
;(3)详见解析.试题分析:(1)根据
 的性质知:让
的性质知:让 解出
解出 的范围,就是单调递增区间;(2)同样根据
的范围,就是单调递增区间;(2)同样根据 的性质:对称轴:
的性质:对称轴: ,解出
,解出 ,对称中心
,对称中心 ,纵坐标为1;解出
,纵坐标为1;解出 ;(3)列表格,根据五点做图,先由确定端点
;(3)列表格,根据五点做图,先由确定端点 时,
时,

 ,
, 时,
时, ,从而确定这之间的五点有
,从而确定这之间的五点有 时,解出对应的
时,解出对应的 ,列出相应的
,列出相应的 值,表格列好,然后在坐标系内,描点,用光滑曲线连接.
值,表格列好,然后在坐标系内,描点,用光滑曲线连接.试题解析:
解:(1)由
 得
得 的单调增区间为
的单调增区间为 . (4)
. (4)(2)由
 得
得 ,即为
,即为 图象的对称轴方程.
图象的对称轴方程.由
 得
得 故
故 图象的对称中心为
图象的对称中心为 .. (4)
.. (4)(3)由
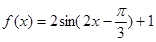 知
知 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 在
在 区间上的图象如图所示.
区间上的图象如图所示. (6)
(6) 的图像和性质;2.五点做图.
的图像和性质;2.五点做图.
练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 .
. 时,求函数
时,求函数 的单调递增区间;
的单调递增区间; 的内角
的内角 的对应边分别为
的对应边分别为 ,且
,且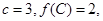 若向量
若向量 与向量
与向量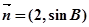 共线,求
共线,求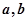 的值.
的值.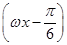 +1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为
+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为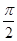 .
.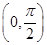 ,f
,f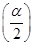 =2,求α的值.
=2,求α的值.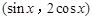 ,b=
,b=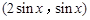 ,设函数
,设函数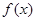 =a
=a b.
b.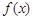 的单调递增区间;
的单调递增区间;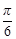 个单位,得到函数
个单位,得到函数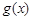 的图象,求函数
的图象,求函数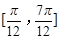 上的最大值和最小值.
上的最大值和最小值. )(ω>0)和g(x)=3cos(2x+φ)的图象的对称中心完全相同,若x∈
)(ω>0)和g(x)=3cos(2x+φ)的图象的对称中心完全相同,若x∈ ,则f(x)的取值范围是______.
,则f(x)的取值范围是______. 在区间
在区间 上的最小值为 ( ).
上的最小值为 ( ).
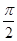 )的图象的一部分如图所示.
)的图象的一部分如图所示.
 时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x的值.
时,求函数y=f(x)+f(x+2)的最大值与最小值及相应的x的值.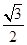 sin ωx-sin2
sin ωx-sin2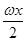 +
+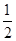 (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.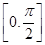 时,求函数f(x)的取值范围.
时,求函数f(x)的取值范围. sin2x的最小正周期T为________.
sin2x的最小正周期T为________.