题目内容
【题目】已知抛物线方程为x2=2py（p＞0），其焦点为F，点O为坐标原点，过焦点F作斜率为k（k≠0）的直线与抛物线交于A，B两点，过A，B两点分别作抛物线的两条切线，设两条切线交于点M．
（1）求 
；
（2）设直线MF与抛物线交于C，D两点，且四边形ACBD的面积为 
，求直线AB的斜率k．
【答案】
（1）解：设直线AB方程为 
，
联立直线AB与抛物线方程
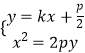，得x2﹣2pkx﹣p2=0，
则x1+x2=2pk，x1x2=﹣p2，
可得 
=x1x2+y1y2=x1x2=x1x2+（kx1+ 
）（kx2+ ）
=（1+k2）x1x2+ 
+ 
（x1+x2）
=（1+k2）（﹣p2）+ + 2pk=﹣ 
p2
（2）解：由x2=2py，知 
，
可得曲线在A，B两点处的切线的斜率分别为 
，
即有AM的方程为 
，BM的方程为 
，
解得交点 
，
则 
，知直线MF与AB相互垂直．
由弦长公式知，|AB|= 
= 
=2p（1+k2），
用 
代k得， 
，
四边形ACBD的面积 
，
依题意，得 的最小值为
，
根据 
的图象和性质得，k2=3或 
，
即 
或 
【解析】（1）设出直线AB的方程，代入抛物线的方程，运用韦达定理和点满足直线方程，由向量的数量积的坐标表示，化简即可得到所求值；（2）求得切线的斜率和切线的方程，运用弦长公式，可得|AB|，|CD|，求得四边形ABCD的面积，运用对勾函数的性质，解方程可得k的值．
练习册系列答案
相关题目
