题目内容
【题目】在四棱锥P﹣ABCD中，底面ABCD是一直角梯形，BA⊥AD，AD∥BC，AB=BC=2，PA=3，PA⊥底面ABCD，E是棱PD上异于P，D的动点．设 
=m，则“0＜m＜2”是三棱锥C﹣ABE的体积不小于1的（ ） 
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【答案】B
【解析】解：经过点E作EH⊥AD，垂足为H，
∵PA⊥底面ABCD，∴平面PAD⊥平面ABCD．
则EH⊥平面ABCD，
∵VC﹣ABE=VE﹣ABC ，
∴VC﹣ABE= 
= 
×EH= 
≥1，
则EH 
，
又PA=3， 
，∴ 
，∴ 
=m≤2﹣1=1，
∴“0＜m＜2”是三棱锥C﹣ABE的体积不小于1的必要不充分条件．
故选：B．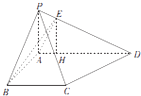
练习册系列答案
阅读快车系列答案
相关题目
