题目内容
11.定义域为(-2,1]的函数f(x)满足f(x+1)=2f(x),且当x∈[0,1]时,f(x)=x2-x.若方程f(x)=m有4个根,则m的取值范围为( )| A. | [-$\frac{1}{4}$,-$\frac{1}{8}$] | B. | (-$\frac{1}{8}$,-$\frac{1}{16}$) | C. | [-$\frac{1}{8}$,-$\frac{1}{16}$] | D. | (-$\frac{1}{4}$,-$\frac{1}{8}$) |
分析 根据题意,求出x∈(-2,-1]时f(x)的解析式,再求f(x)在区间[-2,-1]上的最小值,再求x∈[-1,0]的解析式,求得最小值;求得x∈[0,1]时的解析式,求得最小值,画出f(x)的图象,通过图象观察,y=f(x)的图象和直线y=m有4个交点的情况,即可得到m的范围.
解答 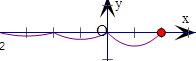 解:当x∈(-2,-1]时,x+2∈(0,1],
解:当x∈(-2,-1]时,x+2∈(0,1],
∴f(x+2)=(x+2)2-(x+2)=x2+3x+2,
又f(x+1)=2f(x),
∴f(x+2)=f[(x+1)+1]=2f(x+1)=4f(x),
∴4f(x)=x2+3x+2(-2<x≤-1),
∴f(x)=$\frac{1}{4}$(x2+3x+2)=$\frac{1}{4}$(x+$\frac{3}{2}$)2-$\frac{1}{16}$(-2<x≤-1),
∴当x=-$\frac{3}{2}$时,f(x)取得最小值-$\frac{1}{16}$;
当x∈[-1,0],则x+1∈[0,1],
故由已知条件可得f(x+1)=(x+1)2-(x+1)=x2+x=2f(x),
∴f(x)=$\frac{1}{2}$(x2+x)=$\frac{1}{2}$(x+$\frac{1}{2}$)2-$\frac{1}{8}$,
故当x=-$\frac{1}{2}$时,函数f(x)取得最小值为-$\frac{1}{8}$,
当x∈[0,1]时,f(x)=x2-x=(x-$\frac{1}{2}$)2-$\frac{1}{4}$,
当x=$\frac{1}{2}$时,取得最小值-$\frac{1}{4}$.
作出函数f(x)在(-2,1]的图象,
方程f(x)=m有4个根,即为y=f(x)与直线y=m有4个交点,
由图象可得-$\frac{1}{8}$<m<-$\frac{1}{16}$,有4个交点.
故选:B.
点评 本题考查函数和方程的转化思想的运用,考查了函数的解析式以及在闭区间上的最值问题,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | -$\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $±\frac{4}{3}$ | D. | $±\frac{3}{4}$ |
