题目内容
已知函数f(x)=ln ax-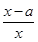 (a≠0).
(a≠0).
(1)求函数f(x)的单调区间及最值;
(2)求证:对于任意正整数n,均有1+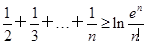 (e为自然对数的底数);
(e为自然对数的底数);
(3)当a=1时,是否存在过点(1,-1)的直线与函数y=f(x)的图象相切?若存在,有多少条?若不存在,请说明理由.
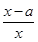 (a≠0).
(a≠0).(1)求函数f(x)的单调区间及最值;
(2)求证:对于任意正整数n,均有1+
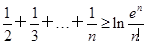 (e为自然对数的底数);
(e为自然对数的底数);(3)当a=1时,是否存在过点(1,-1)的直线与函数y=f(x)的图象相切?若存在,有多少条?若不存在,请说明理由.
(1)当a>0时,函数在(0,a)上是减函数,在(a,+∞)上是增函数,f(x)min=f(a)=ln a2,无最大值.当a<0时,函数在(-∞,a)上是减函数,在(a,0)上是增函数,f(x)min=f(a)=ln a2,无最大值.(2)见解析(3)仅有一根
(1)由题意得f′(x)=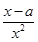 .
.
当a>0时,函数f(x)的定义域为(0,+∞),此时函数在(0,a)上是减函数,在(a,+∞)上是增函数,f(x)min=f(a)=ln a2,无最大值.
当a<0时,函数f(x)的定义域为(-∞,0),此时函数在(-∞,a)上是减函数,在(a,0)上是增函数,f(x)min=f(a)=ln a2,无最大值.
(2)取a=1,由(1)知f(x)=ln x-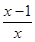 ≥f(1)=0,故
≥f(1)=0,故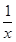 ≥1-ln x=ln
≥1-ln x=ln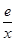 ,
,
取x=1,2,3,…,n,则1+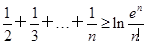 .
.
(3)假设存在这样的切线,设其中一个切点为
T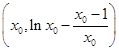 ,∴切线方程为y+1=
,∴切线方程为y+1=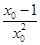 (x-1),将点T坐标代入得ln x0-
(x-1),将点T坐标代入得ln x0-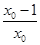 +1=
+1=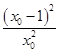 ,即ln x0+
,即ln x0+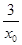 -
-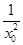 -1=0,①
-1=0,①
设g(x)=ln x+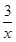 -
-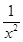 -1,则g′(x)=
-1,则g′(x)=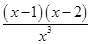 .
.
∵x>0,∴g(x)在区间(0,1),(2,+∞)上是增函数,在区间(1,2)上是减函数,
故g(x)极大值=g(1)=1>0,g(x)极小值=g(2)=ln 2+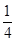 >0.
>0.
又g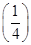 =ln
=ln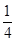 +12-16-1=-ln 4-5<0.
+12-16-1=-ln 4-5<0.
注意到g(x)在其定义域上的单调性,知g(x)=0仅在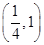 内有且仅有一根,方程①有且仅有一解,故符合条件的切线仅有一条.
内有且仅有一根,方程①有且仅有一解,故符合条件的切线仅有一条.
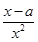 .
.当a>0时,函数f(x)的定义域为(0,+∞),此时函数在(0,a)上是减函数,在(a,+∞)上是增函数,f(x)min=f(a)=ln a2,无最大值.
当a<0时,函数f(x)的定义域为(-∞,0),此时函数在(-∞,a)上是减函数,在(a,0)上是增函数,f(x)min=f(a)=ln a2,无最大值.
(2)取a=1,由(1)知f(x)=ln x-
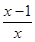 ≥f(1)=0,故
≥f(1)=0,故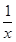 ≥1-ln x=ln
≥1-ln x=ln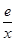 ,
,取x=1,2,3,…,n,则1+
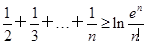 .
.(3)假设存在这样的切线,设其中一个切点为
T
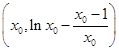 ,∴切线方程为y+1=
,∴切线方程为y+1=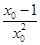 (x-1),将点T坐标代入得ln x0-
(x-1),将点T坐标代入得ln x0-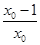 +1=
+1=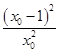 ,即ln x0+
,即ln x0+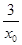 -
-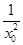 -1=0,①
-1=0,①设g(x)=ln x+
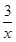 -
-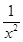 -1,则g′(x)=
-1,则g′(x)=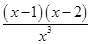 .
.∵x>0,∴g(x)在区间(0,1),(2,+∞)上是增函数,在区间(1,2)上是减函数,
故g(x)极大值=g(1)=1>0,g(x)极小值=g(2)=ln 2+
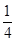 >0.
>0.又g
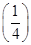 =ln
=ln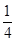 +12-16-1=-ln 4-5<0.
+12-16-1=-ln 4-5<0.注意到g(x)在其定义域上的单调性,知g(x)=0仅在
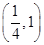 内有且仅有一根,方程①有且仅有一解,故符合条件的切线仅有一条.
内有且仅有一根,方程①有且仅有一解,故符合条件的切线仅有一条.
练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
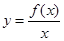 在
在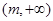 上为增函数(
上为增函数( 为常数),则称
为常数),则称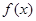 为区间
为区间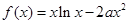 是
是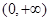 上的“一阶比增函数”,求实数
上的“一阶比增函数”,求实数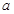 的取值范围;
的取值范围;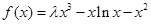 (
(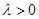 ,
,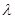 为常数),且
为常数),且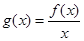 有唯一的零点,求
有唯一的零点,求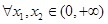 ,
,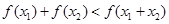
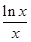 +
+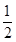 是否有实数解,并说明理由.
是否有实数解,并说明理由.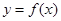 的导数
的导数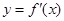 的图像,下列四个结论:
的图像,下列四个结论: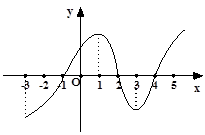
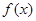 在区间
在区间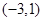 上是增函数;
上是增函数; 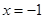 是
是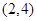 上是减函数,在区间
上是减函数,在区间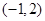 上是增函数;
上是增函数;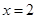 是
是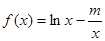 (
(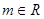 )在区间
)在区间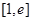 上取得最小值4,则
上取得最小值4,则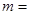 _ __.
_ __.