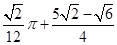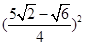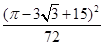题目内容
若函数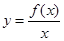 在
在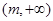 上为增函数(
上为增函数( 为常数),则称
为常数),则称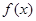 为区间
为区间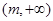 上的“一阶比增函数”,
上的“一阶比增函数”,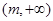 为
为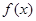 的一阶比增区间.
的一阶比增区间.
(1) 若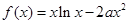 是
是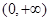 上的“一阶比增函数”,求实数
上的“一阶比增函数”,求实数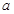 的取值范围;
的取值范围;
(2) 若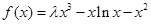 (
(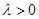 ,
,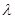 为常数),且
为常数),且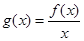 有唯一的零点,求
有唯一的零点,求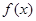 的“一阶比增区间”;
的“一阶比增区间”;
(3)若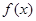 是
是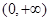 上的“一阶比增函数”,求证:
上的“一阶比增函数”,求证: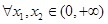 ,
,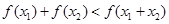
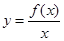 在
在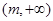 上为增函数(
上为增函数( 为常数),则称
为常数),则称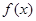 为区间
为区间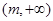 上的“一阶比增函数”,
上的“一阶比增函数”,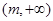 为
为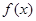 的一阶比增区间.
的一阶比增区间.(1) 若
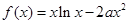 是
是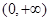 上的“一阶比增函数”,求实数
上的“一阶比增函数”,求实数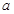 的取值范围;
的取值范围;(2) 若
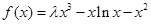 (
(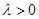 ,
,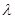 为常数),且
为常数),且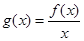 有唯一的零点,求
有唯一的零点,求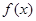 的“一阶比增区间”;
的“一阶比增区间”; (3)若
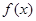 是
是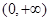 上的“一阶比增函数”,求证:
上的“一阶比增函数”,求证: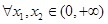 ,
,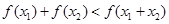
(1) 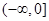 (2)
(2)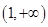
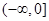 (2)
(2)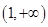
试题分析:
(1)根据新定义可得
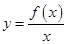 在区间
在区间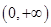 上单调递增,即导函数
上单调递增,即导函数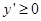 在区间
在区间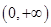 上恒成立,则有
上恒成立,则有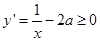 ,再利用分离参数法即可求的a的取值范围.
,再利用分离参数法即可求的a的取值范围.(2)对
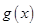 求导数,求单调区间,可以得到函数
求导数,求单调区间,可以得到函数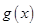 有最小值,又根据函数
有最小值,又根据函数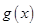 只有一个零点,从而得到
只有一个零点,从而得到 ,解出
,解出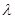 的值为1,再根据
的值为1,再根据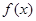 的“一阶比增区间”的定义,则
的“一阶比增区间”的定义,则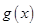 的单调增区间即为
的单调增区间即为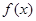 的“一阶比增区间”.
的“一阶比增区间”.(3)根据
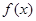 是
是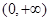 上的“一阶比增函数”的定义,可得到函数
上的“一阶比增函数”的定义,可得到函数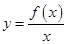 在区间
在区间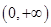 上单调递增,则由函数单调递增的定义可得到
上单调递增,则由函数单调递增的定义可得到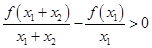 ,同理有
,同理有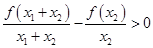 ,两不等式化解相加整理即可得到
,两不等式化解相加整理即可得到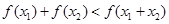 .
.试题解析:
(1)由题得,
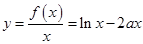 在区间
在区间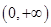 上为增函数,则
上为增函数,则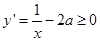 在区间
在区间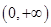 上恒成立,即
上恒成立,即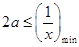
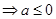 ,综上a的取值范围为
,综上a的取值范围为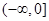 .
.(2)由题得,
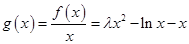 (
(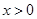 ),则
),则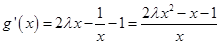 ,当
,当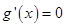 时,因为
时,因为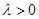 ,所以
,所以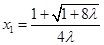 ,
, 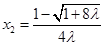 .因为
.因为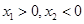 ,所以函数
,所以函数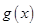 在区间
在区间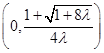 上单调递减,在区间
上单调递减,在区间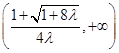 上单调递增,即
上单调递增,即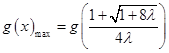 .又因为
.又因为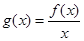 有唯一的零点,所以
有唯一的零点,所以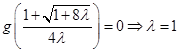 (使
(使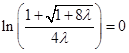 解得
解得 带入验证),故
带入验证),故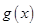 的单调增区间为
的单调增区间为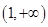 .即
.即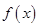 的“一阶比增区间”为
的“一阶比增区间”为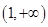 .
.(3)由题得,因为函数
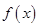 为
为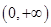 上的“一阶比增函数”,所以
上的“一阶比增函数”,所以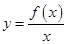 在区间
在区间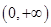 上的增函数,又因为
上的增函数,又因为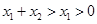 ,所以
,所以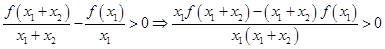
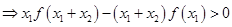 ……1,同理,
……1,同理, 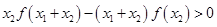 ……2,则1+2得
……2,则1+2得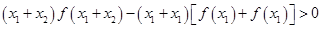
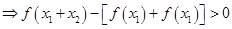
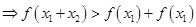 ,所以
,所以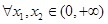 ,
,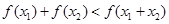 .
.
练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
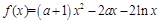 .
.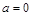 时,
时,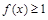 恒成立;
恒成立;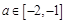 时,求
时,求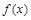 的单调区间.
的单调区间.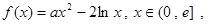 (其中
(其中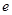 是自然对数的底)
是自然对数的底)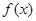 在
在 处取得极值,求
处取得极值,求 的值;
的值;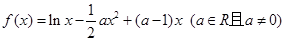
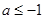 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;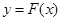 的图象为曲线
的图象为曲线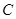 ,设点
,设点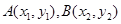 是曲线
是曲线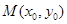 ,使得:①
,使得:①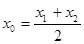 ;②曲线
;②曲线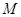 处的切线平行于直线
处的切线平行于直线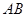 ,则称函数
,则称函数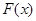 存在“中值相依切线”,试问:函数
存在“中值相依切线”,试问:函数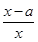 (a≠0).
(a≠0).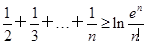 (e为自然对数的底数);
(e为自然对数的底数);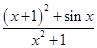 ,其导函数记为f′(x),则f(2 012)+f′(2 012)+f(-2012)-f′(-2012)=________.
,其导函数记为f′(x),则f(2 012)+f′(2 012)+f(-2012)-f′(-2012)=________.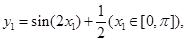 函数
函数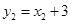 ,则
,则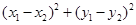 的最小值为( )
的最小值为( )