题目内容
设直线x＝t，与函数f(x)＝x2，g(x)＝ln x的图象分别交于点M，N，则当|MN|达到最小时t的值为________．
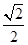
当x＝t时，f(t)＝t2，g(t)＝ln t，
∴y＝|MN|＝t2－ln t(t＞0)．
∴y′＝2t－
＝
＝
.
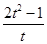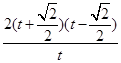当0＜t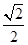＜时，y′＜0；当t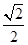＞时，y′＞0.
∴y＝|MN|＝t2－ln t在t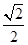＝时有最小值．
∴y＝|MN|＝t2－ln t(t＞0)．
∴y′＝2t－
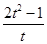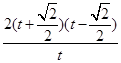＝＝.当0＜t＜
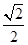时，y′＜0；当t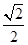＞时，y′＞0.∴y＝|MN|＝t2－ln t在t＝
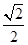时有最小值．
练习册系列答案
相关题目
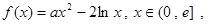(其中
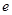是自然对数的底)
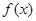在
处取得极值,求
的值；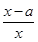
(a≠0)．
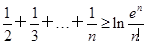(e为自然对数的底数)；
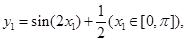函数
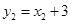,则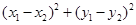
的最小值为( )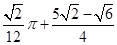 
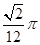
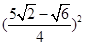
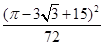
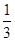ax3－
x2＋cx＋d(a，c，d∈R)满足f(0)＝0，f′(1)＝0，且f′(x)≥0在R上恒成立．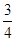
x2－bx＋
－
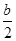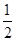x2＋bln (x＋2)在(－1，＋∞)上是减函数，则b的取值范围是________．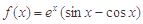
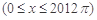，则函数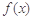
的各极小值之和为 （ ）
