题目内容
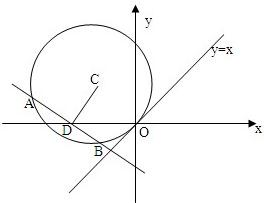
求圆心在l1:y-3x=0上,与x轴相切,且被直线l2:x-y=0截得弦长为4
的圆的方程.
| 7 |
∵圆心在直线y-3x=0上,且与x轴相切,
∴可设圆的圆心为C(a,3a),半径r=|3a|.
圆的方程为(x-a)2+(y-3a)2=9a2,
点C到直线l2:x-y=0的距离为d=
=
|a|,
∵圆C被直线l2:x-y=0截得弦长为4
,
∴根据垂径定理,得
=2
,即
=2
,解之得a=±2,
因此,圆的圆心为(2,6),半径r=6,或圆心为(-2,-6),半径r=6.
所求圆的标准方程为(x-2)2+(y-6)2=36或(x+2)2+(y+6)2=36.
∴可设圆的圆心为C(a,3a),半径r=|3a|.
圆的方程为(x-a)2+(y-3a)2=9a2,
点C到直线l2:x-y=0的距离为d=
| |a-3a| | ||
|
| 2 |
∵圆C被直线l2:x-y=0截得弦长为4
| 7 |
∴根据垂径定理,得
| r2-d2 |
| 7 |
| 9a2-2a2 |
| 7 |
因此,圆的圆心为(2,6),半径r=6,或圆心为(-2,-6),半径r=6.
所求圆的标准方程为(x-2)2+(y-6)2=36或(x+2)2+(y+6)2=36.

练习册系列答案
相关题目
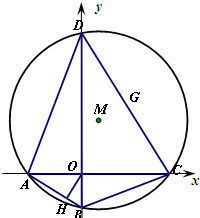
 为中心的双曲线的一条准线方程为
为中心的双曲线的一条准线方程为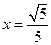 ,离心率
,离心率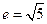 .
.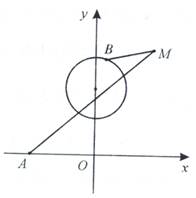
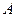 的坐标为
的坐标为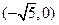 ,
,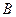 是圆
是圆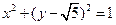 上的点,点
上的点,点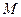 在双曲线右支上,求
在双曲线右支上,求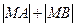 的最小值,并求此时
的最小值,并求此时