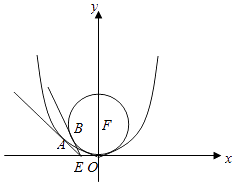题目内容
【题目】如果曲线2|x|﹣y﹣4=0与曲线x2+λy2=4(λ<0)恰好有两个不同的公共点,则实数λ的取值范围是 .
【答案】[﹣ ![]() ,0)
,0)
【解析】解:由2|x|﹣y﹣4=0可得y=2|x|﹣4,
当x≥0时,y=2x﹣4;当x<0时,y=﹣2x﹣4,
∴函数y=2|x|﹣4的图象与方程x2+λy2=4的曲线必相交于(±2,0)
∴为了使函数y=2|x|﹣4的图象与方程x2+λy2=1的曲线恰好有两个不同的公共点,
则y=2x﹣4代入方程x2+λy2=1,整理可得(1+4λ)x2﹣16λx+16λ﹣4=0,
当λ=﹣ ![]() 时,x=2满足题意,由于△>0,2是方程的根,∴
时,x=2满足题意,由于△>0,2是方程的根,∴ ![]() <0,
<0,
解得﹣ ![]() <λ<
<λ< ![]() 时,方程两根异号,满足题意;
时,方程两根异号,满足题意;
y=﹣2x﹣4代入方程x2+λy2=1,整理可得(1+4λ)x2+16λx+16λ﹣4=0
当λ=﹣ ![]() 时,x=﹣2满足题意,由于△>0,﹣1是方程的根,∴
时,x=﹣2满足题意,由于△>0,﹣1是方程的根,∴ ![]() <0,
<0,
解得﹣ ![]() <λ<
<λ< ![]() 时,方程两根异号,满足题意;
时,方程两根异号,满足题意;
∵λ<0,∴实数λ的取值范围是[﹣ ![]() ,0).
,0).
所以答案是[﹣ ![]() ,0).
,0).

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目