题目内容
【题目】若x,y满足 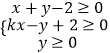 且z=y﹣x的最小值为﹣4,则k的值为( )
且z=y﹣x的最小值为﹣4,则k的值为( )
A.2
B.﹣2
C.![]()
D.﹣ ![]()
【答案】D
【解析】解:对不等式组中的kx﹣y+2≥0讨论,可知直线kx﹣y+2=0与x轴的交点在x+y﹣2=0与x轴的交点的右边, 故由约束条件 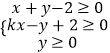 作出可行域如图,
作出可行域如图,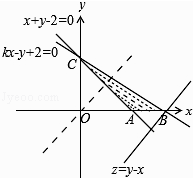
由kx﹣y+2=0,得x= ![]() ,
,
∴B(﹣ ![]() ).
).
由z=y﹣x得y=x+z.
由图可知,当直线y=x+z过B(﹣ ![]() )时直线在y轴上的截距最小,即z最小.
)时直线在y轴上的截距最小,即z最小.
此时 ![]() ,解得:k=﹣
,解得:k=﹣ ![]() .
.
故选:D.
对不等式组中的kx﹣y+2≥0讨论,当k≥0时,可行域内没有使目标函数z=y﹣x取得最小值的最优解,k<0时,若直线kx﹣y+2=0与x轴的交点在x+y﹣2=0与x轴的交点的左边,z=y﹣x的最小值为﹣2,不合题意,由此结合约束条件作出可行域,化目标函数为直线方程的斜截式,由图得到最优解,联立方程组求出最优解的坐标,代入目标函数得答案.

练习册系列答案
相关题目