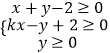题目内容
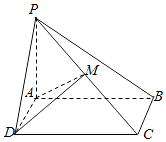
【题目】如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设 ![]() ,
, ![]() ,则得到函数y=f(x).
,则得到函数y=f(x). 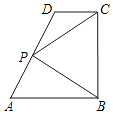
(Ⅰ)求f(1)的值;
(Ⅱ)对于任意a∈(0,+∞),求函数f(x)的最大值.
【答案】解:(1)如图所示,建立直角坐标系.
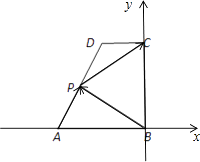
∵在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),
∴B(0,0),A(﹣2,0),D(﹣1,a),C(0,a).
∵ ![]() =x
=x ![]() ,(0≤x≤1).
,(0≤x≤1).
∴ ![]() =
= ![]() +x
+x ![]() =(﹣2,0)+x(1,a)=(x﹣2,xa),
=(﹣2,0)+x(1,a)=(x﹣2,xa),
∴ ![]() =
= ![]() ﹣
﹣ ![]() =(0,a)﹣(x﹣2,xa)=(2﹣x,a﹣xa)
=(0,a)﹣(x﹣2,xa)=(2﹣x,a﹣xa)
∴y=f(x)= ![]()
![]() =(2﹣x,﹣xa)(2﹣x,a﹣xa)
=(2﹣x,﹣xa)(2﹣x,a﹣xa)
=(2﹣x)2﹣ax(a﹣xa)
=(a2+1)x2﹣(4+a2)x+4.
∴f(1)=a2+1﹣(4+a2)+4=1
(Ⅱ)由y=f(x)=(a2+1)x2﹣(4+a2)x+4.
可知:对称轴x0= 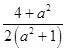 .
.
当0<a≤ ![]() 时,1<x0,∴函数f(x)在[0,1]单调递减,因此当x=0时,函数f(x)取得最大值4.
时,1<x0,∴函数f(x)在[0,1]单调递减,因此当x=0时,函数f(x)取得最大值4.
当a> ![]() 时,0<x0<1,函数f(x)在[0,x0)单调递减,在(x0,1]上单调递增.
时,0<x0<1,函数f(x)在[0,x0)单调递减,在(x0,1]上单调递增.
又f(0)=4,f(1)=1,
∴f(x)max=f(0)=4.
综上所述函数f(x)的最大值为4
【解析】(Ⅰ)画出图形,建立直角坐标系,即得y=f(x)的解析式,代值计算即可(Ⅱ)通过分类讨论,利用二次函数的单调性即可判断出.

练习册系列答案
相关题目