题目内容
20．求下列各式的值：（1）log${\;}_{\frac{1}{3}}$81； （2）lg0.001； （3）log${\;}_{（\sqrt{5}-2）}$（$\sqrt{5}$+2）．
分析 直接利用对数的性质和运算法则求解．
解答 解：（1）log${\;}_{\frac{1}{3}}$81=$\frac{lg81}{lg\frac{1}{3}}$=4lg3$\frac{4lg3}{-lg3}$=-4．
（2）lg0.001=-3．
（3）log${\;}_{（\sqrt{5}-2）}$（$\sqrt{5}$+2）=log${\;}_{（\sqrt{5}-2）}$（$\sqrt{5}$-2）-1=-1．
点评 本题考查对数值的求法，是基础题，解题时要认真审题，注意对数的性质和运算法则的合理运用．
练习册系列答案
相关题目
10．若对于任意实数x∈[e，e2]，不等式$\frac{{e}^{m}}{2}$＞x-$\frac{{e}^{2}}{lnx}$恒成立，则实数的取值范围是 （ ）
| A． | （-∞，-2） | B． | （-∞，2） | C． | （$\frac{1}{2}$，+∞） | D． | （2，+∞） |
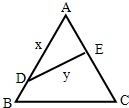如图，某公园有一块边长为2的等边△ABC的边角地，现修成草坪，图中DE把草坪分成面积相等的两部分，D在AB上，E在AC上．