题目内容
设a1,a2,…,an是1,2,…,n的一个排列,把排在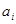 的左边且比
的左边且比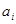 小的数的个数称为
小的数的个数称为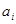 的顺序数(i=1,2,…,n).如:在排列6,4,5,3,2,1中,5的顺序数为1,3的顺序数为0.则在1至8这八个数字构成的全排列中,同时满足8的顺序数为2,7的顺序数为3,5的顺序数为3的不同排列的种数为
的顺序数(i=1,2,…,n).如:在排列6,4,5,3,2,1中,5的顺序数为1,3的顺序数为0.则在1至8这八个数字构成的全排列中,同时满足8的顺序数为2,7的顺序数为3,5的顺序数为3的不同排列的种数为
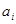 的左边且比
的左边且比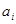 小的数的个数称为
小的数的个数称为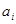 的顺序数(i=1,2,…,n).如:在排列6,4,5,3,2,1中,5的顺序数为1,3的顺序数为0.则在1至8这八个数字构成的全排列中,同时满足8的顺序数为2,7的顺序数为3,5的顺序数为3的不同排列的种数为
的顺序数(i=1,2,…,n).如:在排列6,4,5,3,2,1中,5的顺序数为1,3的顺序数为0.则在1至8这八个数字构成的全排列中,同时满足8的顺序数为2,7的顺序数为3,5的顺序数为3的不同排列的种数为 | A.192 | B.144 | C.96 | D.48 |
B
解:
解:由题意知,8必在第3位,7必在第第5位; 5可以在第6位,5也可以在第7位.
若5在第6位,则5前面有3个空位,需从1、2、3、4中选出3个填上,把剩下的2个数填在5后面的2个空位上,则有: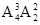 =48种,
=48种,
若5在第7位,则5前面有4个空位,6应填在其中的一个空位上,其它4个数填在剩余的4个位上,则有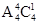 =96种,合计为48+96=144种,
=96种,合计为48+96=144种,
解:由题意知,8必在第3位,7必在第第5位; 5可以在第6位,5也可以在第7位.
若5在第6位,则5前面有3个空位,需从1、2、3、4中选出3个填上,把剩下的2个数填在5后面的2个空位上,则有:
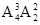 =48种,
=48种,若5在第7位,则5前面有4个空位,6应填在其中的一个空位上,其它4个数填在剩余的4个位上,则有
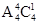 =96种,合计为48+96=144种,
=96种,合计为48+96=144种,
练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
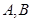 两种必须连排,而
两种必须连排,而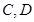 两种不能连排,则不同的排法共有( )
两种不能连排,则不同的排法共有( )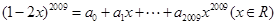 ,则
,则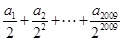 的值为( )
的值为( )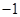
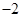
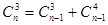 ,则
,则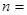 .
.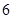
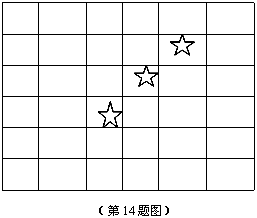
 6的正方形方格的对角线上的3个小方格中分别含有一个五角星,则含有2个五角星的矩形共有
6的正方形方格的对角线上的3个小方格中分别含有一个五角星,则含有2个五角星的矩形共有 个。
个。