题目内容
(本题满分14分)本题共有2个小题,每小题满分各7分.
如图,在四棱锥 中,底面为直角梯形,
中,底面为直角梯形, ,
, 垂直于底面
垂直于底面 ,
, ,
, 分别为
分别为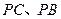 的中点.
的中点.
(1)求证: ;
;
(2)求 与平面
与平面 所成的角.
所成的角.
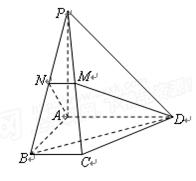
如图,在四棱锥
 中,底面为直角梯形,
中,底面为直角梯形, ,
, 垂直于底面
垂直于底面 ,
, ,
, 分别为
分别为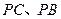 的中点.
的中点. (1)求证:
 ;
;(2)求
 与平面
与平面 所成的角.
所成的角.
略
解法一:(1)以 点为坐标原点建立空间直角坐标系
点为坐标原点建立空间直角坐标系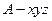 (图略),由
(图略),由 得
得
 ,
, ,
, ,
,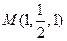
 (2分)
(2分)
因为 (5分) 所以
(5分) 所以 . (7分)
. (7分)
(2)因为
 ,所以
,所以 ,又
,又 ,
,
故 平面
平面 ,即
,即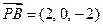 是平面
是平面 的法向量.(
的法向量.( 9分)
9分)
设 与平面
与平面 所成的角为
所成的角为 ,又
,又 ,设
,设 与
与 夹角为
夹角为 ,
,
则 , (12分)
, (12分)
又 ,故
,故
 ,故
,故 与平面
与平面 所成的角是
所成的角是 . (14分)
. (14分)
解法二:(1)证明:因为 是
是 的中点,
的中点, , 所以
, 所以 (2分)
(2分)
由 底面
底面 ,得
,得 ,又
,又 ,即
,即 ,
,
 平面
平面 ,
, (4
(4 分)
分)  面
面 ,
, (7分)
(7分)
(2)联结 ,
, 平面
平面 ,故
,故 为
为 与面
与面 所成角(9分)
所成角(9分)
在 中,
中, ,
,
在 中,
中,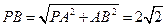 ,故
,故 ,
,
在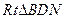 中,
中,  ,又
,又 , (12分)
, (12分)
故 与平面
与平面 所成的角是
所成的角是 (14分)
(14分)
 点为坐标原点建立空间直角坐标系
点为坐标原点建立空间直角坐标系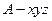 (图略),由
(图略),由 得
得 ,
, ,
, ,
,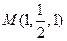
 (2分)
(2分)因为
 (5分) 所以
(5分) 所以 . (7分)
. (7分)(2)因为

 ,所以
,所以 ,又
,又 ,
,故
 平面
平面 ,即
,即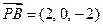 是平面
是平面 的法向量.(
的法向量.( 9分)
9分)设
 与平面
与平面 所成的角为
所成的角为 ,又
,又 ,设
,设 与
与 夹角为
夹角为 ,
,则
 , (12分)
, (12分)又
 ,故
,故
 ,故
,故 与平面
与平面 所成的角是
所成的角是 . (14分)
. (14分)解法二:(1)证明:因为
 是
是 的中点,
的中点, , 所以
, 所以 (2分)
(2分)由
 底面
底面 ,得
,得 ,又
,又 ,即
,即 ,
,
 平面
平面 ,
, (4
(4 分)
分)  面
面 ,
, (7分)
(7分)(2)联结
 ,
, 平面
平面 ,故
,故 为
为 与面
与面 所成角(9分)
所成角(9分)
在
 中,
中, ,
,在
 中,
中,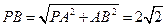 ,故
,故 ,
,在
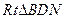 中,
中,  ,又
,又 , (12分)
, (12分)故
 与平面
与平面 所成的角是
所成的角是 (14分)
(14分)
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的三条侧棱
的三条侧棱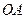 、
、 、
、 两两垂直,且长度均为2.
两两垂直,且长度均为2. 、
、 分别是
分别是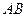 、
、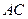 的中点,
的中点, 是
是 的中点,过
的中点,过 、
、 、
、 ,已知
,已知 .
. ⊥面
⊥面 ;
; 的大小.
的大小.
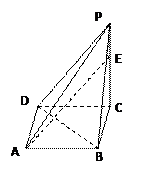 (2)是否不论点E 在何位置都有BD⊥AE,证明你的结论。
(2)是否不论点E 在何位置都有BD⊥AE,证明你的结论。
 、
、 、
、 是表面积为
是表面积为 的球面上三点,
的球面上三点, ,
, ,
, ,
, 为球心,则直线
为球心,则直线 与截面
与截面 所成的角是( )
所成的角是( )

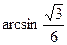

 ,
,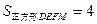 ,求
,求



 .
. 图如右,根据图中标出的尺寸
图如右,根据图中标出的尺寸

 (
( )学
)学