题目内容
已知向量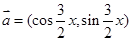 ,
,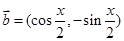 ,且
,且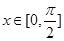 .
.
求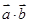 及
及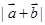 ;
;
若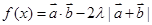 的最小值是
的最小值是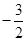 ,求实数
,求实数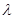 的值;
的值;
设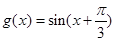 ,若方程
,若方程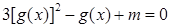 在
在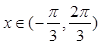 内有两个不同的解,求实数
内有两个不同的解,求实数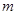 的取值范围.
的取值范围.
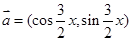 ,
,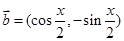 ,且
,且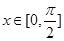 .
.求
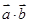 及
及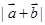 ;
;若
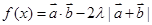 的最小值是
的最小值是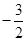 ,求实数
,求实数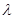 的值;
的值;设
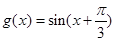 ,若方程
,若方程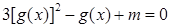 在
在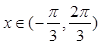 内有两个不同的解,求实数
内有两个不同的解,求实数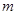 的取值范围.
的取值范围.(1)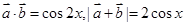 ;(2)
;(2)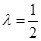 ;(3)
;(3)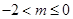 或
或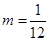 .
.
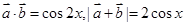 ;(2)
;(2)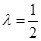 ;(3)
;(3)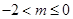 或
或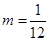 .
.试题分析:(1)根据已知条件及平面向量的坐标表示与模的坐标表示,
可以得到
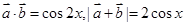 ;
;由(1)可得,原问题等价为求使
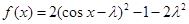 的最小值为
的最小值为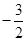 的
的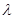 的值,这是一个二次函数与三角函数的复合函数,需分别讨论以下三种情况:①
的值,这是一个二次函数与三角函数的复合函数,需分别讨论以下三种情况:①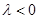 ,②
,②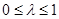 ,③
,③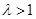 下
下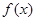 取得最小值的情况,从而可以得到
取得最小值的情况,从而可以得到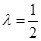 ;(3)当
;(3)当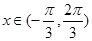 时,
时,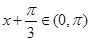 ,
,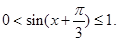 根据正弦函数
根据正弦函数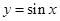 在
在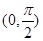 及
及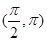 上取值的对称性,设
上取值的对称性,设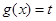 ,要保证题中方程有两个不同的解,必须保证方程
,要保证题中方程有两个不同的解,必须保证方程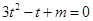 ,在
,在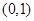 仅有一根或有两个相等根,由一元二次方程根的分布,可得
仅有一根或有两个相等根,由一元二次方程根的分布,可得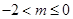 或
或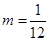 .
.(1)∵
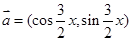 ,
,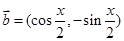 ,
,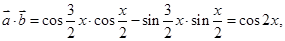
∴
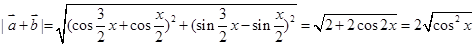
∵
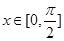 , ∴
, ∴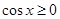 ∴
∴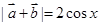 4分
4分(2)由(1)得
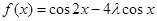 ,即
,即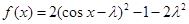
∵
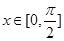 , ∴
, ∴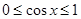
①当
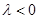 时,当且仅当
时,当且仅当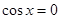 时,
时,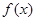 取得最小值
取得最小值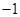 ,这与已知矛盾.
,这与已知矛盾.②当
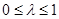 时,当且仅当
时,当且仅当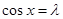 时,
时,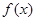 取最小值
取最小值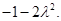
由已知得
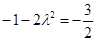 ,解得
,解得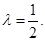
③当
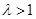 时,当且仅当
时,当且仅当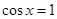 时,
时,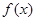 取得最小值
取得最小值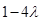 .
.由已知得
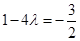 ,解得
,解得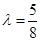 ,这与
,这与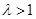 相矛盾.
相矛盾.综上所述,
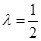 为所求. 9分;
为所求. 9分;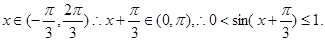 根据正弦函数
根据正弦函数 在
在 及
及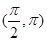 上取值的对称性,因此设
上取值的对称性,因此设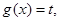 问题等价于方程
问题等价于方程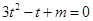 ,在
,在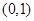 仅有一根或有两个相等根,∴
仅有一根或有两个相等根,∴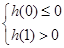 或
或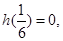 ∴
∴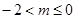 或
或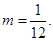
综上,
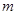 的取值范围是:
的取值范围是: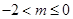 或
或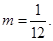 14分.
14分.
练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
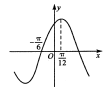
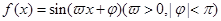 的部分图像,则
的部分图像,则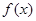 的解析式为
的解析式为 .
.
 x﹣
x﹣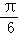 ),x∈R.
),x∈R.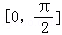 ,f(3
,f(3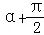 )=
)=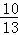 ,f(3β+
,f(3β+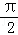 )=
)=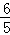 .求sin(α+β)的值.
.求sin(α+β)的值.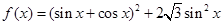 .
.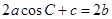 ,求f(B)的取值范围.
,求f(B)的取值范围.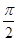 )的最小正周期是π,若其图象向右平移
)的最小正周期是π,若其图象向右平移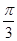 个单位后得到的函数为奇函数,则函数f(x)的图象( )
个单位后得到的函数为奇函数,则函数f(x)的图象( )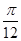 ,0)对称
,0)对称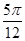 ,0)对称
,0)对称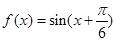 +
+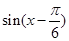 +
+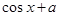 (
(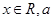 为常数)
为常数)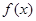 的最小正周期;
的最小正周期;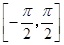 上的最大值与最小值之和为
上的最大值与最小值之和为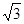 ,求实数
,求实数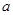 的值.
的值.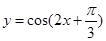 的图象,只需将函数
的图象,只需将函数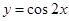 的图象上各点( )
的图象上各点( )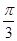 个长度单位
个长度单位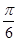 个长度单位
个长度单位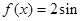
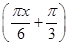
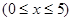 ,点A、B分别是函数
,点A、B分别是函数 图像上的最高点和最低点.
图像上的最高点和最低点.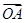 ·
· 的值;
的值; 、
、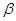 的终边上,求tan(
的终边上,求tan(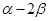 )的值.
)的值.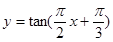 的定义域是 .
的定义域是 .