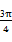题目内容
(12分)(2011•广东)已知函数f(x)=2sin( x﹣
x﹣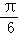 ),x∈R.
),x∈R.
(1)求f(0)的值;
(2)设α,β∈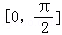 ,f(3
,f(3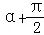 )=
)=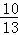 ,f(3β+
,f(3β+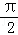 )=
)=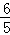 .求sin(α+β)的值.
.求sin(α+β)的值.
 x﹣
x﹣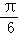 ),x∈R.
),x∈R.(1)求f(0)的值;
(2)设α,β∈
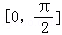 ,f(3
,f(3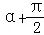 )=
)=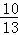 ,f(3β+
,f(3β+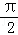 )=
)=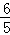 .求sin(α+β)的值.
.求sin(α+β)的值.(1)﹣1(2)

试题分析:(1)把x=0代入函数解析式求解.
(2)根据题意可分别求得sinα和sinβ的值,进而利用同角三角函数基本关系求得cosα和cosβ的值,最后利用正弦的两角和公式求得答案.
解:(1)f(0)=2sin(﹣
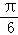 )=﹣1
)=﹣1(2)f(3
 )=2sinα=
)=2sinα= ,f(3β+
,f(3β+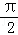 )=2sinβ=
)=2sinβ=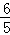 .
.∴sinα=
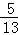 ,sinβ=
,sinβ=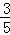
∵α,β∈
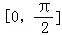 ,
,∴cosα=
 =
=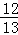 ,cosβ=
,cosβ=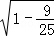 =
=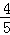
∴sin(α+β)=sinαcosβ+cosαsinβ=

点评:本题主要考查了两角和与差的正弦函数.考查了对三角函数基础公式的熟练记忆.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
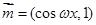 ,
,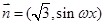 (
(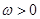 ),函数
),函数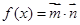 ,且
,且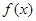 图象上一个最高点为
图象上一个最高点为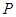
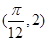 ,与
,与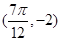 .
.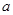 为常数,判断方程
为常数,判断方程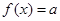 在区间
在区间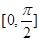 上的解的个数;
上的解的个数; 中,若
中,若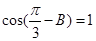 ,求
,求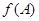 的取值范围.
的取值范围.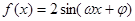 (其中
(其中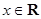 ,
,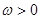 ,
,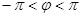 )的部分图象如图所示,则函数f(x)的解析式是 .
)的部分图象如图所示,则函数f(x)的解析式是 .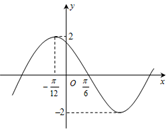
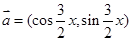 ,
,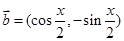 ,且
,且 .
.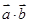 及
及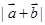 ;
;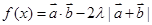 的最小值是
的最小值是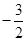 ,求实数
,求实数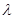 的值;
的值;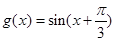 ,若方程
,若方程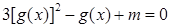 在
在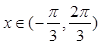 内有两个不同的解,求实数
内有两个不同的解,求实数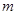 的取值范围.
的取值范围. )的图象向左平移
)的图象向左平移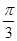 ,2)
,2) ,2)
,2) ,2)
,2)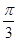 ,x=
,x=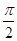 都是函数f(x)=sin(ωx+φ)(ω>0,-π<φ≤π)的对称轴,且函数f(x)在区间
都是函数f(x)=sin(ωx+φ)(ω>0,-π<φ≤π)的对称轴,且函数f(x)在区间 上单调递减,则( )
上单调递减,则( ) ,而
,而 .
. 最大,求
最大,求 能取到的最小正数值.
能取到的最小正数值.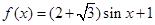 且
且 ,求
,求 .
. 的图象关于直线
的图象关于直线 对称,则
对称,则 可能是( )
可能是( )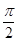




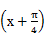 的图象沿x轴向右平移a个单位(a>0),所得图象关于y轴对称,则a的最小值为( )
的图象沿x轴向右平移a个单位(a>0),所得图象关于y轴对称,则a的最小值为( )