Question

【题目】已知数列{xn}满足x1=1，x2=λ，并且 =λ （λ为非零常数，n=2，3，4，…）． （Ⅰ）若x1 ， x3 ， x5成等比数列，求λ的值；
（Ⅱ）设0＜λ＜1，常数k∈N* ， 证明 ．

Answer 1

【答案】解：（I）∵x1=1，x2=λ，并且 =λ （λ为非零常数，n=2，3，4，…）． ∴x3= =λ3 ， x4= 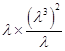=λ6 ， x5= =λ10 ．
∵x1 ， x3 ， x5成等比数列，
∴ =x1x5 ，
∴（λ3）2=1×λ10 ， λ≠0，
化为λ4=1，
解得λ=±1．
（II）证明：设0＜λ＜1，常数k∈N* ， =λ ， =λ．
∴ =λλn﹣1=λn ，
∴xn= … x1=λn﹣1λn﹣2…λ1= ．
∴ = = ．
∴ + +…+ = + +…+ = ＜ ＜ ．
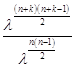【解析】（I）由于x1=1，x2=λ，并且 =λ （λ为非零常数，n=2，3，4，…）．可得x3 ， x4 ， x5 ． 由于x1 ， x3 ， x5成等比数列，可得 =x1x5 ， 代入解出即可得出．（II）设0＜λ＜1，常数k∈N* ， =λ ， =λ．可得 =λn ， 利用“累乘求积”可得：xn= … x1= ．可得 = ．再利用等比数列的前n项和公式即可得出．
【考点精析】解答此题的关键在于理解等比数列的通项公式（及其变式）的相关知识，掌握通项公式：．