Question

【题目】已知sin（x﹣ ）= ，cos2x= ， （Ⅰ）求 的值；
（Ⅱ）求 的值．

Answer 1

【答案】解：（Ⅰ）∵sin（x﹣ ）= ， （sinx﹣cosx）= ，
sinx﹣cosx= ①，
1﹣2sinxcosx= ，
sinxcosx=﹣ ②，
∴由①②可得：cox＜0，
又∵cos2x=2cos2x﹣1= ，解得：cosx=﹣ ，由①可得：sinx= ，
∴
=cos（ + ﹣x）
=cos cos（ ﹣x）﹣sin sin（ ﹣x）
= cos（x﹣ ）+ sin（x﹣ ）
= × （﹣ + ）+ ×
= ．
（Ⅱ）∵由（Ⅰ）可得：cosx=﹣ ，sinx= ，
∴ = =﹣
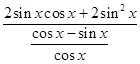【解析】（Ⅰ）由已知等式利用特殊角的三角函数值，两角差的正弦函数公式化简可得sinx﹣cosx= ，两边平方可得sinxcosx=﹣ ，结合cos2x= ，利用二倍角的余弦函数公式可求cosx，sinx的值， 由特殊角的三角函数值，两角和与差的余弦函数公式即可化简求值．（Ⅱ）由（Ⅰ）cosx，sinx的值，利用同角三角函数基本关系式，倍角公式即可化简求值．