题目内容
6.已知锐角三角形的边长分别为1,3,a,则a的范围是( )| A. | (8,10) | B. | (2$\sqrt{2}$,$\sqrt{10}$) | C. | (2$\sqrt{2}$,10) | D. | ($\sqrt{10}$,8) |
分析 由已知中△ABC三边长分别为1、3、a,根据余弦定理的推论得到△ABC为锐角三角形时,由两边长1和3求出a的范围,但3与a边均有可能为最大边,故要分类讨论.
解答 解:∵△ABC三边长分别为1、3、a,
又∵△ABC为锐角三角形,
当3为最大边时,a≤3,设3所对的角为α,
则根据余弦定理得:cosα=$\frac{{a}^{2}+1-9}{2a}$>0,
∵a>0,∴a2-8>0,
解得:2$\sqrt{2}$<a≤3;
当a为最大边时a>3,设a所对的角为β,
则根据余弦定理得:cosβ=$\frac{1+9-{a}^{2}}{6}$>0,
∴10-a2>0,解得:3<a<$\sqrt{10}$,
综上,实数a的取值范围为(2$\sqrt{2}$,$\sqrt{10}$),
故选:B.
点评 此题考查了余弦定理,利用了分类讨论的思想.解答本题的关键是利用余弦定理推论出最大边所对角的余弦值大于0,进而根据两边长1和2求出第三边a的取值范围.

练习册系列答案
相关题目
11.与直线x+2y-4=0在x轴上的截距相同,与直线xtan$\frac{2π}{3}$+y-4=0的倾斜角相同的直线方程为( )
| A. | $\sqrt{3}$x-y-4=0 | B. | $\sqrt{3}$x-y-4$\sqrt{3}$=0 | C. | $\sqrt{3}$x+y-4=0 | D. | $\sqrt{3}$x+y-4$\sqrt{3}$=0 |
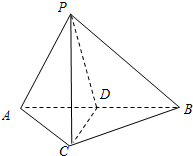 如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.