题目内容
14.化简:(1)3$\sqrt{15}$sinx+3$\sqrt{5}$cosx;
(2)$\frac{3}{2}$cosx-$\frac{\sqrt{3}}{2}$sinx;
(3)$\sqrt{3}$sin$\frac{x}{2}$+cos$\frac{x}{2}$;
(4)$\frac{\sqrt{2}}{4}$sin($\frac{π}{4}$-x)+$\frac{\sqrt{6}}{4}$cos($\frac{π}{4}$-x);
(5)sin164°sin224°+sin254°sin314°;
(6)sin(α+β)cos(γ-β)-cos(β+α)sin(β-γ);
(7)sin(α-β)sin(β-γ)-cos(α-β)cos(γ-β);
(8)tan$\frac{5π}{4}$+tan$\frac{5π}{12}$.
分析 根据两角和与差的正弦,余弦及正切公式,结合诱导公式,特殊角的三角函数,逐一化简,可得答案.
解答 解:(1)3$\sqrt{15}$sinx+3$\sqrt{5}$cosx=6$\sqrt{5}$($\frac{\sqrt{3}}{2}$sinx+$\frac{1}{2}$cosx)=6$\sqrt{5}$(sinxcos$\frac{π}{6}$+cosxsin$\frac{π}{6}$)=6$\sqrt{5}$sin(x+$\frac{π}{6}$);
(2)$\frac{3}{2}$cosx-$\frac{\sqrt{3}}{2}$sinx=$\sqrt{3}$($\frac{\sqrt{3}}{2}$cosx-$\frac{1}{2}$sinx)=$\sqrt{3}$(cos$\frac{π}{6}$cosx-sin$\frac{π}{6}$sinx)=$\sqrt{3}$cos(x+$\frac{π}{6}$);
(3)$\sqrt{3}$sin$\frac{x}{2}$+cos$\frac{x}{2}$=2($\frac{\sqrt{3}}{2}$sin$\frac{x}{2}$+$\frac{1}{2}$cos$\frac{x}{2}$)=2(sin$\frac{x}{2}$cos$\frac{π}{6}$+cos$\frac{x}{2}$sin$\frac{π}{6}$)=2sin($\frac{x}{2}$+$\frac{π}{6}$);
(4)$\frac{\sqrt{2}}{4}$sin($\frac{π}{4}$-x)+$\frac{\sqrt{6}}{4}$cos($\frac{π}{4}$-x)=$\frac{\sqrt{2}}{2}$[$\frac{1}{2}$sin($\frac{π}{4}$-x)+$\frac{\sqrt{3}}{2}$cos($\frac{π}{4}$-x)]=$\frac{\sqrt{2}}{2}$[sin($\frac{π}{4}$-x)cos$\frac{π}{3}$+cos($\frac{π}{4}$-x)sin$\frac{π}{3}$]=$\frac{\sqrt{2}}{2}$sin($\frac{π}{4}$-x+$\frac{π}{3}$)=$\frac{\sqrt{2}}{2}$sin($\frac{7π}{12}$-x);
(5)sin164°sin224°+sin254°sin314°=sin(180°-16°)sin(180°+44°)+sin(270°-16°)sin(270°+44°)=-sin16°sin44°+cos16°cos44°=cos(44°+16°)=cos60°=$\frac{1}{2}$;
(6)sin(α+β)cos(γ-β)-cos(β+α)sin(β-γ)=sin(α+β)cos(β-γ)-cos(α+β)sin(β-γ)=sin[(α+β)-(β-γ)]=sin(α+γ);
(7)sin(α-β)sin(β-γ)-cos(α-β)cos(γ-β)=sin(α-β)sin(β-γ)-cos(α-β)cos(β-γ)=cos[(α-β)+(β-γ)]=cos(α-γ);
(8)tan$\frac{5π}{4}$+tan$\frac{5π}{12}$=tan(π+$\frac{π}{4}$)+tan($\frac{π}{6}$+$\frac{π}{4}$)=tan$\frac{π}{4}$+$\frac{tan\frac{π}{6}+tan\frac{π}{4}}{1-tan\frac{π}{6}tan\frac{π}{4}}$=1+$\frac{1+\frac{\sqrt{3}}{3}}{1-\frac{\sqrt{3}}{3}}$=3+$\sqrt{3}$.
点评 本题考查的知识点是两角和与差的正弦,余弦及正切公式,难度不大,属于基础题.

 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案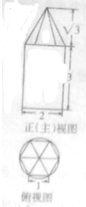 某几何体的正视图与俯视图如图所示,若俯视图中的多边形为正六边形,则该几何体的侧视图的面积为( )
某几何体的正视图与俯视图如图所示,若俯视图中的多边形为正六边形,则该几何体的侧视图的面积为( )| A. | $\frac{15}{2}$ | B. | 6+$\sqrt{3}$ | C. | $\frac{3}{2}$+3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
| A. | (8,10) | B. | (2$\sqrt{2}$,$\sqrt{10}$) | C. | (2$\sqrt{2}$,10) | D. | ($\sqrt{10}$,8) |
 销售甲,乙两种商品所得到利润与投入资金x(万元)的关系分别为f(x)=m$\sqrt{x+1}+a$,g(x)=bx(其中m,a,b∈R),函数f(x),g(x)对应的曲线C1,C2,如图所示.
销售甲,乙两种商品所得到利润与投入资金x(万元)的关系分别为f(x)=m$\sqrt{x+1}+a$,g(x)=bx(其中m,a,b∈R),函数f(x),g(x)对应的曲线C1,C2,如图所示.