题目内容
【题目】给定实数 t,已知命题 p:函数![]() 有零点;命题 q: x∈[1,+∞)
有零点;命题 q: x∈[1,+∞) ![]() ≤4
≤4![]() -1.
-1.
(Ⅰ)当 t=1 时,判断命题 q 的真假;
(Ⅱ)若 p∨q 为假命题,求 t 的取值范围.
【答案】(1)命题 q 为真命题.
(2)![]()
![]() .
.
【解析】
(1) t=1 时,![]() ,进而得到结果;(2)若 p∨q 为假命题,则 p,q 都是假命题,当 p 为假命题时,Δ=
,进而得到结果;(2)若 p∨q 为假命题,则 p,q 都是假命题,当 p 为假命题时,Δ=![]() -4<0 ,q 为真命题时,
-4<0 ,q 为真命题时,![]() ≤
≤![]() -1,即 4
-1,即 4![]() -1≥0,取补集即可得到q 为假命题时,
-1≥0,取补集即可得到q 为假命题时,![]()
![]() ,最终两者取交集.
,最终两者取交集.
(Ⅰ)当 t=1 时,![]()
![]() ≤3 在[1,+∞)上恒成立,故命题 q 为真命题.
≤3 在[1,+∞)上恒成立,故命题 q 为真命题.
(Ⅱ)若 p∨q 为假命题,则 p,q 都是假命题.
当 p 为假命题时,Δ=![]() -4<0,解得-1<t<1;
-4<0,解得-1<t<1;
当 q 为真命题时,![]() ≤4
≤4![]() -1,即
-1,即![]() -1≥0,解得 t≤
-1≥0,解得 t≤![]() 或 t≥
或 t≥![]()
∴当 q 为假命题时,![]()
![]()
∴t 的取值范围是![]()
![]() .
.

 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案【题目】现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率:先由计算器给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,
9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:
7527 | 0293 | 7140 | 9857 | 0347 | 4373 | 8636 | 6947 | 1417 | 4698 |
0371 | 6233 | 2616 | 8045 | 6011 | 3661 | 9597 | 7424 | 7610 | 4281 |
根据以上数据估计该射击运动员射击4次至少击中3次的概率为_______.
【题目】在统计学中,偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差,班主任为了了解个别学生的偏科情况,对学生数学偏差x(单位:分)与物理偏差y(单位:分)之间的关系进行学科偏差分析,决定从全班56位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如下:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学偏差x | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
物理偏差y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
(1)已知x与y之间具有线性相关关系,求y关于x的线性回归方程;
(2)若这次考试该班数学平均分为118分,物理平均分为90.5,试预测数学成绩126分的同学的物理成绩.
参考公式: 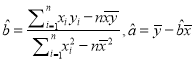 .
.
参考数据: ![]() .
.