题目内容
(本题12分)
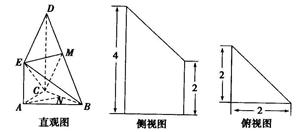
如图的几何体中,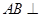 平面
平面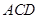 ,
,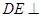 平面
平面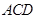 ,△
,△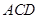 为等边三角形,
为等边三角形, 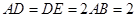 ,
,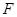 为
为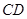 的中点.
的中点.
(1)求证: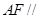 平面
平面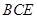 ;
;
(2)求证:平面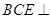 平面
平面 ;
;
(3)求此几何体的体积。
(1)只需证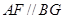 ;(2)只需证BG⊥平面
;(2)只需证BG⊥平面 ;(3)
;(3)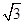 。
。
解析试题分析:证明:取 的中点
的中点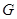 ,连结
,连结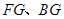 .∵
.∵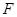 为
为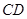 的中点,∴
的中点,∴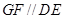 且
且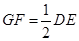 .
.
∵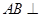 平面
平面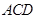 ,
,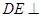 平面
平面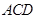 , ∴
, ∴ ,∴
,∴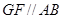 .
.
又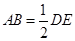 ,∴
,∴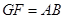 . ∴四边形
. ∴四边形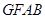 为平行四边形,则
为平行四边形,则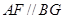 .
.
∵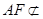 平面
平面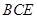 ,
,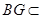 平面
平面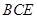 , ∴
, ∴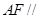 平面
平面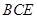 .…………4分
.…………4分 8分
8分
(3)解:取DE的中点M连BM,GM所以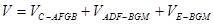
=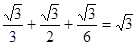 或
或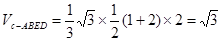 …………12分
…………12分
考点:线面垂直的性质定理;线面平行的判断定理;面面垂直的判定定理;四棱锥的体积公式。
点评:证明线面平行的常用方法:
①定义:若一条直线和一个平面没有公共点,则它们平行;
②线线平行Þ线面平行
若平面外的一条直线平行于平面内的一条直线,则它与这个平面平行。 即
即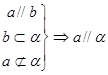
③面面平行Þ线面平行
若两平面平行,则其中一个平面内的任一条直线平行于另一个平面。 即
即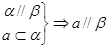

练习册系列答案
相关题目
 的底面为直角梯形,
的底面为直角梯形,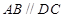 ,
,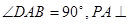 底面
底面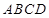 ,且
,且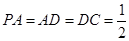 ,
,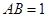 ,
,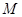 是
是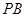 的中点。
的中点。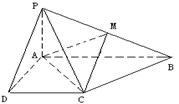
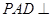 面
面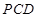 ;
;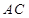 与
与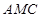 与面
与面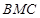 所成二面角的大小。
所成二面角的大小。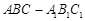 中,
中,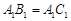 ,
,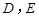 分 别是棱
分 别是棱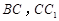 上的点(点
上的点(点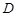 不同于点
不同于点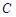 ),且
),且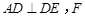 为
为 的中点.
的中点.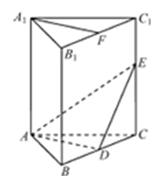
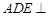 平面
平面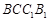 (2)直线
(2)直线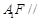 平面
平面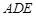
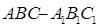 中,点M、N分别为线段
中,点M、N分别为线段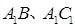 的中点,平面
的中点,平面
 侧面
侧面
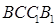 (2)证明:BC
(2)证明:BC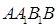
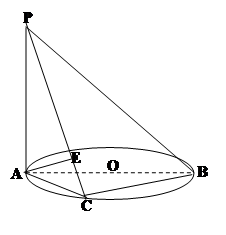
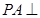 ⊙O所在的平面,AB是⊙O的直径,C是⊙O上任意一点,过A作
⊙O所在的平面,AB是⊙O的直径,C是⊙O上任意一点,过A作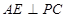 于E,求证:
于E,求证: .
. 
 满足
满足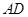 ∥
∥ ,
,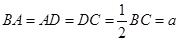 ,
, 是
是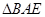 沿着
沿着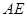 翻折成
翻折成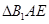 ,使面
,使面 面
面 ,
,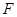 为
为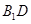 的中点.
的中点. 
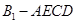 的体积;(Ⅱ)证明:
的体积;(Ⅱ)证明: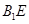 ∥面
∥面 ;
; 与面
与面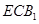 所成二面角的余弦值.
所成二面角的余弦值.