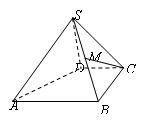
题目内容
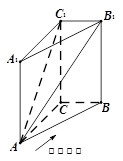
(本题12分)如图,已知正四棱柱ABCD—A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F,
⑵ 证:平面A1CB⊥平面BDE;
⑵求A1B与平面BDE所成角的正弦值。
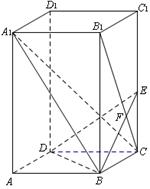
由正四棱柱得BD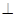 AC,BD
AC,BD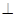 AA1,推出BD
AA1,推出BD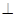 面A1 AC ,A1C
面A1 AC ,A1C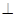 BD ,又A1B1
BD ,又A1B1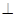 面BB1 C1C,BE得到BE
面BB1 C1C,BE得到BE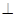 A1B1,又BE
A1B1,又BE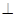 B1C, BE
B1C, BE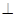 面A1B1C,平面A1CB⊥平面BDE;;
面A1B1C,平面A1CB⊥平面BDE;;
⑵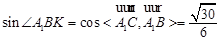
解析试题分析: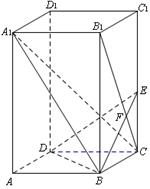
正四棱柱得BD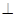 AC,BD
AC,BD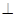 AA1,又
AA1,又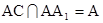 ,
, BD
BD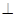 面A1 AC ,又A1 C
面A1 AC ,又A1 C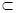 面A1 AC,
面A1 AC, A1C
A1C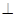 BD ,又A1B1
BD ,又A1B1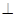 面BB1 C1C,BE
面BB1 C1C,BE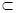 面BB1 C1C,
面BB1 C1C,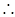 BE
BE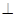 A1B1,又BE
A1B1,又BE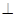 B1C,
B1C,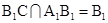
 BE
BE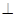 面A1B1C,A1 C
面A1B1C,A1 C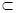 面A1B1C,
面A1B1C, BE
BE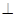 A1 C,又
A1 C,又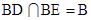 ,
,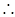 A1 C
A1 C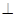 面BDE,又A1 C
面BDE,又A1 C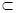 面A1BC
面A1BC 平面A1CB⊥平面BDE;
平面A1CB⊥平面BDE;
⑵以DA、DC、DD1分别为x、y、z轴,建立坐标系,则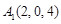 ,
,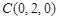 ,
,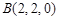 ,
,
∴ ,
,
∴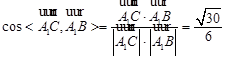 ,设A1C
,设A1C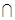 平面BDE=K,由⑴可知,∠A1BK为A1B与平面BDE所成角,∴
平面BDE=K,由⑴可知,∠A1BK为A1B与平面BDE所成角,∴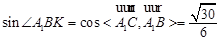
考点:本题主要考查立体几何中的平行关系、垂直关系,角的计算。
点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,利用向量则能简化证明过程。本题通过建立空间直角坐标系,利用向量的坐标运算,简化了证明过程。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的三视图和直观图如图所示.
的三视图和直观图如图所示.
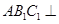 平面
平面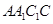 ;
;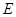 是线段
是线段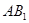 上的一点,且满足
上的一点,且满足 ,求
,求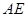 的长.
的长.
 的直观图及三视图如图所示,
的直观图及三视图如图所示, 分别为
分别为 的中点.
的中点.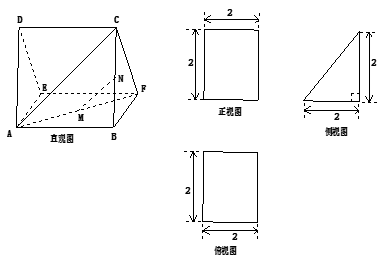
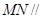 平面
平面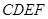 ;
;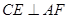 ;
;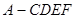 的体积。
的体积。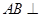 平面
平面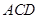 ,
,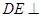 平面
平面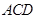 ,△
,△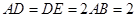 ,
,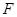 为
为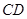 的中点.
的中点.
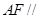 平面
平面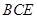 ;
;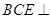 平面
平面 ;
;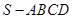 中,
中,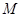 是
是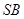 的中点,
的中点,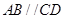 ,
,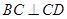 ,且
,且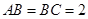 ,
,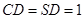 ,又
,又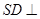 面
面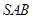 .
.
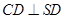 ;
; 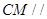 面
面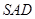 ;
; 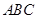 的中位线
的中位线 ,将平面
,将平面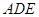 折起,平面
折起,平面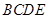 ,得到四棱锥
,得到四棱锥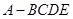 ,
,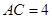 ,设
,设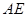 、
、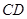 的中点分别为
的中点分别为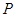 、
、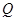 ,
,