题目内容
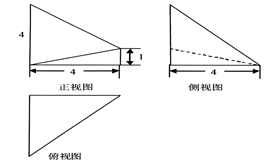
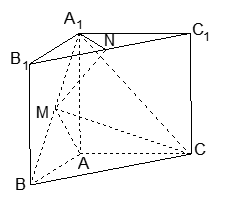
(本小题满分13分)如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图,俯视图,在直观图中,M是BD的中点,N是BC的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.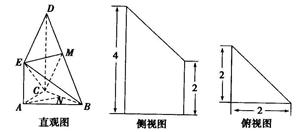
(1)求该几何体的体积;
(2)求证:AN∥平面CME;
(3)求证:平面BDE⊥平面BCD
(1)4 ;(2)连接MN,则MN∥CD,且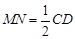 .又AE∥CD,且
.又AE∥CD,且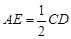 ,
,
∴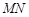 ∥
∥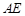 ,
,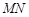 =
=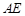 ∴四边形ANME为平行四边形,∴AN∥EM.∵AN
∴四边形ANME为平行四边形,∴AN∥EM.∵AN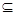 平面CME,EM
平面CME,EM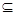 平面CME,∴AN∥平面CME (3)∵AC=AB,N是BC的中点,∴AN⊥BC,又平面ABC⊥平面BCD,∴AN⊥平面BCD则(2)知:AN∥EM,∴EM⊥平面BCD,又EM
平面CME,∴AN∥平面CME (3)∵AC=AB,N是BC的中点,∴AN⊥BC,又平面ABC⊥平面BCD,∴AN⊥平面BCD则(2)知:AN∥EM,∴EM⊥平面BCD,又EM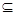 平面BDE,∴平面BDE⊥平面BCD
平面BDE,∴平面BDE⊥平面BCD
解析试题分析:(1)由题意可知:四棱锥B-ACDE中,平面ABC⊥平面ACDE,AB⊥AC,
AB⊥平面ACDE,又AC=AB=AE=2,CD=4, …………2分
则四棱锥B-ACDE的体积为: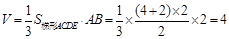 ,
,
即该几何体的体积为4 …………4分
(2)证明:由题图知,连接MN,则MN∥CD,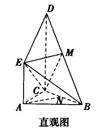
且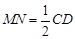 .又AE∥CD,且
.又AE∥CD,且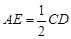 , …………6分
, …………6分
∴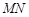 ∥
∥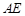 ,
,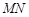 =
=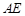 ∴四边形ANME为平行四边形,∴AN∥EM.
∴四边形ANME为平行四边形,∴AN∥EM.
∵AN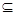 平面CME,EM
平面CME,EM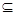 平面CME,∴AN∥平面CME ……………8分
平面CME,∴AN∥平面CME ……………8分
(3)证明:∵AC=AB,N是BC的中点,∴AN⊥BC,
又平面ABC⊥平面BCD,∴AN⊥平面BCD …………10分
则(2)知:AN∥EM,
∴EM⊥平面BCD,又EM 平面BDE,∴平面BDE⊥平面BCD ……13分
平面BDE,∴平面BDE⊥平面BCD ……13分
考点:本题考查了空间中的线面关系
点评:高考中常考查空间中平行关系与垂直关系的证明以及几何体体积的计算,这是高考的重点内容.证明的关键是熟练掌握并灵活运用相关的判定定理与性质定理.

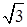 ,AD=CD=1.
,AD=CD=1.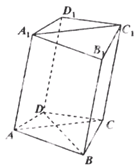
 求证:BD⊥AA1;
求证:BD⊥AA1; 若四边形
若四边形 是菱形,且
是菱形,且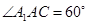 ,求四棱柱
,求四棱柱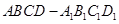 的体积.
的体积.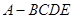 的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.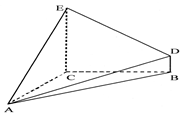
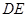 与
与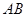 所成角的余弦值;
所成角的余弦值;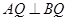 ,并说明理由.
,并说明理由.
 ,且
,且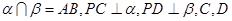 是垂足,
是垂足,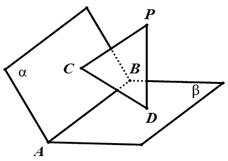
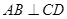
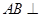 平面
平面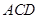 ,
,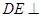 平面
平面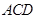 ,△
,△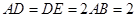 ,
,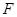 为
为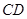 的中点.
的中点.
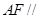 平面
平面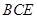 ;
;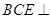 平面
平面 ;
;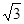 ,侧棱长是3,点E、F分别在BB1、DD1上,且AE⊥A1B,AF⊥A1D.
,侧棱长是3,点E、F分别在BB1、DD1上,且AE⊥A1B,AF⊥A1D.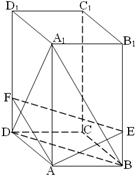
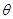 的正切值.
的正切值.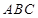
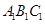 中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
,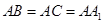
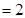 ,点
,点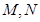 分别为
分别为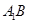 和
和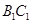 的中点.
的中点.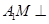 平面
平面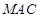 ;
;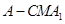 的体积;
的体积;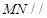 平面
平面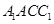 .
.
 满足
满足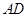 ∥
∥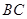 ,
,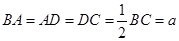 ,
,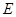 是
是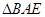 沿着
沿着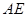 翻折成
翻折成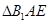 ,使面
,使面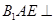 面
面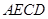 ,
, 为
为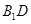 的中点.
的中点. 
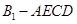 的体积;(Ⅱ)证明:
的体积;(Ⅱ)证明: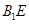 ∥面
∥面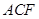 ;
;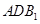 与面
与面 所成二面角的余弦值.
所成二面角的余弦值.