题目内容
【题目】在某次数学考试中，抽查了1000名学生的成绩，得到频率分布直方图如图所示，规定85分及其以上为优秀.
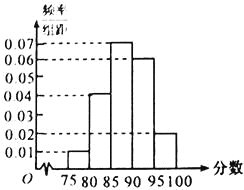
（1）下表是这次抽查成绩的频数分布表，试求正整数
、
的值；
区间 | [75，80） | [80，85） | [85，90） | [90，95） | [95，100] |
人数 | 50 | a | 350 | 300 | b |
（2）现在要用分层抽样的方法从这1000人中抽取40人的成绩进行分析，求抽取成绩为优秀的学生人数；
（3）在根据（2）抽取的40名学生中，要随机选取2名学生参加座谈会，记其中成绩为优秀的人数为X，求X的分布列与数学期望（即均值）.
【答案】（1）
；（2）
人；（3）数学期望为
.
【解析】
试题（1）从所给出的频率分布直方图中可知80分至85分所占的频率为
，那么
；95分至100分所占的频率为
，所以
.（2）根据分层抽样可以得到抽取成绩为优秀的学生人数为30人；（3）优秀人数X的所有可能取值分别为
人，
人，
人.先计算出
,那么可以列出其分布列，然后计算出所对应的数学期望
.
试题解析：（1）80分至85分的人数为：
（人）；
95分至100分的人数为：
（人）；
（2）用分层抽样的方法从1000人中抽取40人，其中成绩为优秀的学生人数为：
（人）；
（3）在抽取的40人中，85分以下的共有10人，85分及其以上的共有30人，从中抽取的2人中，
成绩优秀的人数X的可能取值分别是：0人、1人、2人，其分布列如下表：
X | 0 | 1 | 2 |
P(X) |
|
|
|
X的数学期望为：
练习册系列答案
相关题目
