题目内容
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() 为边
为边![]() 的中点,以
的中点,以![]() 为折痕把
为折痕把![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且使平面
的位置,且使平面![]() 平面
平面![]() .
.
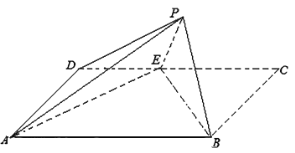
(1)证明:![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据已知条件,得到![]() ,即
,即![]() ,由平面
,由平面![]() 平面
平面![]() ,得到
,得到![]() 平面
平面![]() ,从而得到
,从而得到![]() ,结合
,结合![]() 得到
得到![]() 平面
平面![]() ;(2)过点
;(2)过点![]() 在平面
在平面![]() 中向
中向![]() 引垂线,垂足
引垂线,垂足![]() ,连接
,连接![]() 和
和![]() ,得到
,得到![]() 和
和![]() 的长,由平面
的长,由平面![]() 平面
平面![]() ,得到
,得到![]() ,从而得到
,从而得到![]() ,
,![]() 的长,设
的长,设![]() 为
为![]() 的中点,在等腰三角形
的中点,在等腰三角形![]() 中,求出
中,求出![]() 的长,利用
的长,利用![]() ,求出点
,求出点![]() 到平面
到平面![]() 的距离.
的距离.
(1)因为在矩形![]() 中,
中,![]() ,
,![]() 为边
为边![]() 的中点,
的中点,
所以![]() ,又
,又![]() ,所以
,所以![]()
所以![]() ,
,
又平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,![]() 平面
平面![]()
所以![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,
,
故![]() ,
,
又![]() ,且
,且![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)过点![]() 在平面
在平面![]() 中向
中向![]() 引垂线,垂足
引垂线,垂足![]() ,连接
,连接![]() 和
和![]() ,
,
由![]() 得
得![]() 为
为![]() 的中点,
的中点,
所以![]() ,
,![]() ,
,
由平面![]() 平面
平面![]() ,
,![]() ,
,
![]() 面
面![]() ,平面
,平面![]() 平面
平面![]()
所以![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,
,
所以![]() ,
,![]() ,
,
故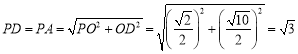 ,
,
设![]() 为
为![]() 的中点,连接
的中点,连接![]() ,在等腰三角形
,在等腰三角形![]() 中,
中,
![]() ,
,
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
由![]() ,得
,得![]() ,
,
即![]()
![]() ,
,
解得![]() .
.

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
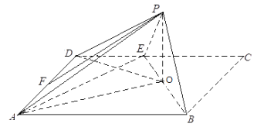
浙江之星学业水平测试系列答案【题目】某县一中学的同学为了解本县成年人的交通安全意识情况,利用假期进行了一次全县成年人安全知识抽样调查.已知该县成年人中![]() 的拥有驾驶证,先根据是否拥有驾驶证,用分层抽样的方法抽取了100名成年人,然后对这100人进行问卷调查,所得分数的频率分布直方图如下图所示.规定分数在80以上(含80)的为“安全意识优秀”.
的拥有驾驶证,先根据是否拥有驾驶证,用分层抽样的方法抽取了100名成年人,然后对这100人进行问卷调查,所得分数的频率分布直方图如下图所示.规定分数在80以上(含80)的为“安全意识优秀”.
拥有驾驶证 | 没有驾驶证 | 合计 | |
得分优秀 | |||
得分不优秀 | 25 | ||
合计 | 100 |

(1)补全上面![]() 的列联表,并判断能否有超过
的列联表,并判断能否有超过![]() 的把握认为“安全意识优秀与是否拥有驾驶证”有关?
的把握认为“安全意识优秀与是否拥有驾驶证”有关?
(2)若规定参加调查的100人中分数在70以上(含70)的为“安全意识优良”,从参加调查的100人中根据安全意识是否优良,按分层抽样的方法抽出5人,再从5人中随机抽取3人,试求抽取的3人中恰有一人为“安全意识优良”的概率.
附表及公式: ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】在某次数学考试中,抽查了1000名学生的成绩,得到频率分布直方图如图所示,规定85分及其以上为优秀.
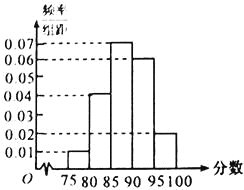
(1)下表是这次抽查成绩的频数分布表,试求正整数![]() 、
、![]() 的值;
的值;
区间 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
人数 | 50 | a | 350 | 300 | b |
(2)现在要用分层抽样的方法从这1000人中抽取40人的成绩进行分析,求抽取成绩为优秀的学生人数;
(3)在根据(2)抽取的40名学生中,要随机选取2名学生参加座谈会,记其中成绩为优秀的人数为X,求X的分布列与数学期望(即均值).
【题目】中国历法推测遵循以测为辅、以算为主的原则.例如《周髀算经》和《易经》里对二十四节气的晷(guǐ)影长的记录中,冬至和夏至的晷影长是实测得到的,其它节气的晷影长则使按照等差数列的规律计算得出的,下表为《周髀算经》对二十四节气晷影长的记录,其中![]() 寸表示115寸
寸表示115寸![]() 分(1寸
分(1寸![]() 分),已知《易经》中记录的冬至晷影长为130.0寸,夏至晷影长为14.8寸,那么《易经》中所记录的惊蛰的晷影长应为( )
分),已知《易经》中记录的冬至晷影长为130.0寸,夏至晷影长为14.8寸,那么《易经》中所记录的惊蛰的晷影长应为( )
节气 | 冬至 | 小寒(大雪) | 大寒(小雪) | 立春(立冬) | 雨水(霜降) | 惊蛰(寒露) |
晷影(寸) | 135 |
|
|
|
|
|
节气 | 春分(秋分) | 清明(白露) | 谷雨(处暑) | 立夏(立秋) | 小满(大暑) | 芒种(小暑) | 夏至 |
晷影(寸) | 75.5 |
|
|
|
|
| 16.0 |
A.72.4寸B.81.4寸C.82.0寸D.91.6寸
