Question

【题目】【2017北京丰台5月综合测试】已知函数.

（Ⅰ）当时，求曲线在点处的切线方程；

（Ⅱ）证明：对于，在区间上有极小值，且极小值大于0.

Answer 1

【答案】（1）（2）见解析

【解析】

（Ⅰ）的定义域为，

因为，所以，所以.

因为，，

所以曲线在点处的切线方程为.

（Ⅱ）因为,所以在区间上是单调递增函数.

因为，，

所以,使得.

所以，；，，

故在上单调递减，在上单调递增，

所以有极小值.

因为,

所以.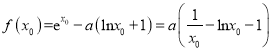

设，，

则，

所以，即在上单调递减，所以，

即，所以函数的极小值大于0．

点睛:本题考查导数的几何意义以及函数的单调性与极值问题.函数y＝f（x）在x＝x0处的导数的几何意义，就是曲线y＝f（x）在点P（x0，y0）处的切线的斜率，过点P的切线方程为：.求函数y＝f（x）在点P（x0，y0）处的切线方程与求函数y＝f（x）过点P（x0，y0）的切线方程意义不同，前者切线有且只有一条，且方程为y－y0＝f′（x0）（x－x0），后者可能不只一条．