题目内容
【题目】某通讯公司需要在三角形地带OAC区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域BOC内,乙中转站建在区域AOB内.分界线OB固定,且OB=(1+ ![]() )百米,边界线AC始终过点B,边界线OA、OC满足∠AOC=75°,∠AOB=30°,∠BOC=45°.设OA=x(3≤x≤6)百米,OC=y百米.
)百米,边界线AC始终过点B,边界线OA、OC满足∠AOC=75°,∠AOB=30°,∠BOC=45°.设OA=x(3≤x≤6)百米,OC=y百米.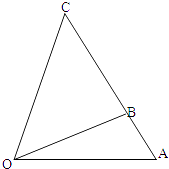
(1)试将y表示成x的函数,并求出函数y的解析式;
(2)当x取何值时?整个中转站的占地面积S△OAC最小,并求出其面积的最小值.
【答案】
(1)
解:结合图形可知,S△BOC+S△AOB=S△AOC.
于是, ![]() x(1+
x(1+ ![]() )sin30°+
)sin30°+ ![]() y(1+
y(1+ ![]() )sin45°=
)sin45°= ![]() xysin75°,
xysin75°,
解得:y= ![]() ,(其中3≤x≤6)
,(其中3≤x≤6)
(2)
解:由(1)知,y= ![]() (3≤x≤6),
(3≤x≤6),
因此,S△AOC= ![]() xysin75°
xysin75°
= ![]()
![]()
= ![]() [(x﹣2)+
[(x﹣2)+ ![]() +4]
+4]
≥2+2 ![]() (当且仅当x﹣2=
(当且仅当x﹣2= ![]() ,即x=4时,等号成立).
,即x=4时,等号成立).
∴当x=400米时,整个中转站的占地面积S△OAC最小,最小面积是(2+2 ![]() )×104平方米.
)×104平方米.
【解析】(1)由图形知,S△BOC+S△AOB=S△AOC , 代入面积公式,求出函数y的解析式;(2)由(1)知,函数y的解析式,求出S△AOC的表达式,利用基本不等式求出S△OAC最小时,x的取值以及最小面积是什么.

【题目】从某大学一年级女生中,选取身高分别是150cm、155cm、160cm、165cm、170cm的学生各一名,其身高和体重数据如表所示:
身高/cm(x) | 150 | 155 | 160 | 165 | 170 |
体重/kg(y) | 43 | 46 | 49 | 51 | 56 |
(1)求y关于x的线性回归方程;
(2)利用(1)中的回归方程,计算身高为168cm时,体重的估计值 ![]() 为多少?
为多少?
参考公式:线性回归方程 ![]() =
= ![]() x+
x+ ![]() ,其中
,其中 ![]() =
=  =
= 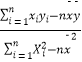 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.