题目内容
【题目】已知函数![]() ,当x = -1时取得极大值7,当x = 3时取得极小值;
,当x = -1时取得极大值7,当x = 3时取得极小值;
(1)求a,b的值;
(2)求f(x)的极小值。
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
利用函数f(x)在x=x0取得极值的充要条件f′(x0)=0且f′(x)在x=x0的左右附近符号相反即可得出a,b的值,再利用极大值即可得到c,从而得出答案.
(1)∵f(x) = x3+ ax2+bx + c ,∴f′ (x) = 3x2+2ax +b
∵当x =- 1 时函数取得极大值7,当x = 3时取得极小值
∴x =- 1 和x = 3是方程f′ (x)=0的两根,有
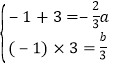 ∴
∴![]() , ∴f(x) = x3-3x2-9x+c.
, ∴f(x) = x3-3x2-9x+c.
(2)∵当x = -1时,函数取极大值7,∴(-1)3–3(-1)2–9(-1)+c= 7,∴c=2.
此时函数f(x)的极小值为:f(3)= 33-3×32-9×3×2=-25.

练习册系列答案
相关题目
