��Ŀ����
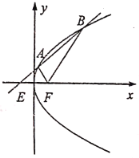
����Ŀ���̲����н��ܣ�Բ![]() �ϵĵ�
�ϵĵ�![]() �������߷���Ϊ
�������߷���Ϊ![]() .���ǽ�������ƹ㣺��Բ
.���ǽ�������ƹ㣺��Բ![]() ��
��![]() ���ϵĵ�
���ϵĵ�![]() �������߷���Ϊ
�������߷���Ϊ![]() ���ڽⱾ��ʱ����ֱ��Ӧ��.��֪��ֱ��
���ڽⱾ��ʱ����ֱ��Ӧ��.��֪��ֱ��![]() ����Բ
����Բ![]() ��
��![]() ��
��![]() ������ֻ��һ��������.
������ֻ��һ��������.
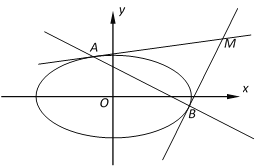
��1������Բ![]() �ķ��̣�
�ķ��̣�
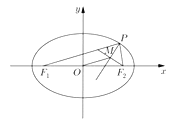
��2����![]() Ϊ����ԭ�㣬����Բ
Ϊ����ԭ�㣬����Բ![]() �ϵ�����
�ϵ�����![]() ��
��![]() �ֱ�������Բ����������
�ֱ�������Բ����������![]() ��
��![]() ����
����![]() ��
��![]() ���ڵ�
���ڵ�![]() .��
.��![]() �仯ʱ����
�仯ʱ����![]() ��������ֵ��
��������ֵ��
��3����![]() ����Բ
����Բ![]()
![]() �ϲ�ͬ�����㣬
�ϲ�ͬ�����㣬![]()
![]() �ᣬԲ
�ᣬԲ![]() ��
��![]() ����Բ
����Բ![]() ������һ�㶼����Բ
������һ�㶼����Բ![]() �ڣ����Բ
�ڣ����Բ![]() Ϊ����Բ��һ������Բ.���ʣ���Բ
Ϊ����Բ��һ������Բ.���ʣ���Բ![]() �Ƿ���ڹ���
�Ƿ���ڹ���![]() ������Բ�������ڣ����Բ��
������Բ�������ڣ����Բ��![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2��
����2��![]() ����3�����ڣ�
����3�����ڣ�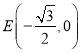
��������
��1����ֱ��![]() ������Բ���̣��õ�
������Բ���̣��õ�![]() �ķ��̣���ֱ�ߺ���Բ���е��������б�ʽΪ0���ⷽ�̿ɵ�
�ķ��̣���ֱ�ߺ���Բ���е��������б�ʽΪ0���ⷽ�̿ɵ�![]() ��ֵ��
��ֵ��
��2�����е�![]() ���ɵ�����
���ɵ�����![]() ������
������![]() ������ʽ���������ȷ��һ��ֱ�ߣ��ɵ��е��ҷ��̣�����
������ʽ���������ȷ��һ��ֱ�ߣ��ɵ��е��ҷ��̣�����![]() ��б�ʣ���������б�ʹ�ʽ���ɢٿɵ�
��б�ʣ���������б�ʹ�ʽ���ɢٿɵ�![]() �ķ���Ϊ
�ķ���Ϊ![]() �����õ㵽ֱ�ߵľ��빫ʽ��ֱ������Բ��������������Τ�ﶨ�����ҳ���ʽ�����
�����õ㵽ֱ�ߵľ��빫ʽ��ֱ������Բ��������������Τ�ﶨ�����ҳ���ʽ�����![]() ��������������������û�������ʽ���ɵõ��������ֵ��
��������������������û�������ʽ���ɵõ��������ֵ��
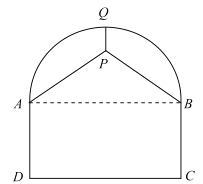
��3��������ɵ÷���Ҫ���Բ![]() ����Ϊ����
����Ϊ����![]() �������ε����Բ.����Բ����
�������ε����Բ.����Բ����![]() ����.��������д��Բ
����.��������д��Բ![]() �ķ���.����Բ�Ĵ��ڱ���Ҫ���ϣ���Բ�ϵĵ㵽Բ
�ķ���.����Բ�Ĵ��ڱ���Ҫ���ϣ���Բ�ϵĵ㵽Բ![]() �������Сֵ��
�������Сֵ��![]() �����ͼ�οɵ�Բ��
�����ͼ�οɵ�Բ��![]() ���߶�
���߶�![]() �ϣ��뾶��С.�����ڵ�
�ϣ��뾶��С.�����ڵ�![]() ��֪��������ý���.
��֪��������ý���.
�⣺��1����ֱ��![]() ������Բ����
������Բ����![]() ��
��
�ɵ�![]() ��
��
��ֱ�ߺ���Բ���У��ɵ�![]() ��
��
���![]() ����
����![]() ����
����
������Բ![]() �ķ���Ϊ
�ķ���Ϊ![]() ��
��
��2�����е�![]() ��
��
�ɵ�����![]() ��
��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ���ɵ�
���ɵ�![]() ��
��
������ȷ��һ��ֱ�ߣ��ɵ�![]() �ķ���Ϊ
�ķ���Ϊ![]() ��
��
��Ϊ![]() ��
��
ԭ�㵽ֱ��![]() �ľ���Ϊ
�ľ���Ϊ![]() ��
��
��![]() ��ȥ
��ȥ![]() ���ɵ�
���ɵ�![]() ��
��![]() ��
��
�ɵ�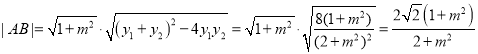 ��
��
�ɵ�![]() �����
�����![]() ��
��
��![]() ��
��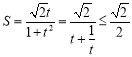 ��
��
���ҽ���![]() ��
��![]() ʱ��
ʱ��![]() ȡ�����ֵ
ȡ�����ֵ![]() ��
��
��3����Բ�ĶԳ��ԣ�������![]() ����
����![]() ��
��![]() ���ϣ����
���ϣ����![]() ��
��
��Բ![]() �ķ���Ϊ��
�ķ���Ϊ��![]() ��
��
������Բ����֪������Բ�ϵĵ㵽��![]() �������Сֵ��
�������Сֵ��![]() ��
��
���![]() ����Բ
����Բ![]() ������һ�㣬
������һ�㣬
��![]() ��
��
��![]() ʱ��
ʱ��![]() ��С��
��С��![]() ���٣�
���٣�
��Բ![]() ����
����![]() ��
��![]() ����
����
��![]() ����Բ�ϣ�
����Բ�ϣ�![]() ����
����
�ɢ٢ڢۣ���ã�![]() ��
��![]() ��
��
��![]() ʱ��
ʱ��![]() ���������⣬
���������⣬
���ϣ���Բ![]() ���ڷ�������������Բ����
���ڷ�������������Բ����![]() ��������
��������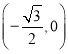 .
.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�