题目内容
12.若函数f(x)=ax+log4(4x+1)为偶函数,则a=-$\frac{1}{2}$.分析 利用函数为偶函数的定义寻找关于k的方程是求解本题的关键,转化过程中要注意对数的运算性质的运用.
解答 解:(1)由函数f(x)是偶函数,可知f(x)=f(-x)
∴log4(4x+1)+ax=log4(4-x+1)-ax
即$lo{g}_{4}\frac{{4}^{x}+1}{{4}^{-x}+1}$=-2ax,
∴log44x=-2ax
∴x=-2ax对一切x∈R恒成立,
∴a=-$\frac{1}{2}$
故答案为:-$\frac{1}{2}$.
点评 本题考查函数为偶函数的定义,考查对数的运算性质,考查学生的转化与化归思想,注意学生的运算整理变形的等价性.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
3.下列命题中的真命题是( )
| A. | ?x0∈R,使得${e^{x_0}}≤0$ | B. | ?x∈R,x2+1<3x | ||
| C. | ?x0∈R,使得|x0-3|+|x0-1|<2 | D. | ?x>0,x+$\frac{4}{x}$≥4 |
4.给定两个单位平面向量$\overrightarrow{OA},\overrightarrow{OB}$,其夹角为120°,以O为圆心的圆弧AB上任一点,且$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$(x,y∈R),则满足x+y≥$\sqrt{2}$的概率为( )
| A. | $2-\sqrt{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{2}{3}$ |
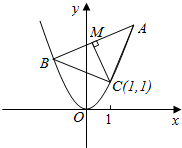 过抛物线y=x2上定点C(1,1)引两条互相垂直的弦CA、CB,作CM⊥AB,M为垂足,求点M的轨迹方程.
过抛物线y=x2上定点C(1,1)引两条互相垂直的弦CA、CB,作CM⊥AB,M为垂足,求点M的轨迹方程.