题目内容
【题目】在平面直角坐标系xOy中,椭圆C的参数方程为 ![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为 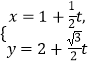 (t为参数).
(t为参数).
(Ⅰ)写出椭圆C的普通方程和直线l的倾斜角;
(Ⅱ)若点P(1,2),设直线l与椭圆C相交于A,B两点,求|PA|·|PB|的值.
【答案】解:(Ⅰ)消去θ得到椭圆C的普通方程为 ![]() .
.
∵直线 ![]() 的斜率为
的斜率为 ![]() ,∴直线l的倾斜角为
,∴直线l的倾斜角为 ![]() .
.
(Ⅱ)把直线 ![]() 的方程
的方程 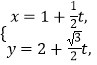 ,代入
,代入 ![]() 中,
中,
得 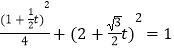 .
.
即 ![]() ,
,
∴t1·t2=4,即|PA|·|PB|=4.
【解析】(Ⅰ)利用sin2θ+cos2θ=1消去θ,从而得到椭圆的普通方程,根据参数方程可知直线l定过点(1,2),从而斜率为![]() ,即为
,即为![]() ,从而求得直线l的倾斜角;(Ⅱ)因为
,从而求得直线l的倾斜角;(Ⅱ)因为![]() ,所以|PA|·|PB|=t1·t2=4.
,所以|PA|·|PB|=t1·t2=4.
【考点精析】根据题目的已知条件,利用直线的倾斜角和椭圆的标准方程的相关知识可以得到问题的答案,需要掌握当直线l与x轴相交时, 取x轴作为基准, x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角.特别地,当直线l与x轴平行或重合时, 规定α=0°;椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.

练习册系列答案
相关题目