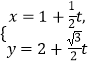题目内容
【题目】设![]() 是公差不为零的等差数列,满足
是公差不为零的等差数列,满足![]() 数列
数列![]() 的通项公式为
的通项公式为![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)将数列![]() ,
,![]() 中的公共项按从小到大的顺序构成数列
中的公共项按从小到大的顺序构成数列![]() ,请直接写出数列
,请直接写出数列![]() 的通项公式;
的通项公式;
(3)记![]() ,是否存在正整数
,是否存在正整数![]()
![]() ,使得
,使得![]() 成等差数列?若存在,求出
成等差数列?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]() (3)存在正整数m=11,n=1;m=2,n=3;m=6,n=11使得b2,bm,bn成等差数列
(3)存在正整数m=11,n=1;m=2,n=3;m=6,n=11使得b2,bm,bn成等差数列
【解析】试题分析:(1)利用基本元的思想,将已知条件转化为![]() 的形式,解方程组求得
的形式,解方程组求得![]()
![]() 的值,并求得
的值,并求得![]() 的通项公式.(2)由于
的通项公式.(2)由于![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,且
的等差数列,且![]() ,而
,而![]() 是,首项为
是,首项为![]() ,第二项为
,第二项为![]() 的等差数列,故
的等差数列,故![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,故通项公式为
的等差数列,故通项公式为![]() .(3)
.(3) ![]() ,先假设存在这样的数
,先假设存在这样的数![]() ,利用
,利用![]() 成等差数列,化简得到
成等差数列,化简得到![]() ,利用列举法求得
,利用列举法求得![]() 的值.
的值.
试题解析:
(1)设公差为![]() ,则
,则![]() ,由性质得
,由性质得![]() ,因为
,因为![]() ,所以
,所以![]() ,即
,即![]() ,又由
,又由![]() 得
得![]() ,解得
,解得![]() ,
,
![]() 所以
所以![]() 的通项公式为
的通项公式为![]()
(2) ![]()
(3),假设存在正整数m、n,使得d5,dm,dn成等差数列,则d5+dn=2dm. ![]()
所以![]() +
+![]() =
=![]() , 化简得:2m=13-
, 化简得:2m=13-![]() .
.
当n-2=-1,即n=1时,m=11,符合题意;
当n-2=1,即n=3时,m=2,符合题意
当n-2=3,即n=5时,m=5(舍去) ;
当n-2=9,即n=11时,m=6,符合题意.
所以存在正整数m=11,n=1;m=2,n=3;m=6,n=11
使得b2,bm,bn成等差数列.

练习册系列答案
相关题目