题目内容
【题目】如图,![]() 、
、![]() 分别为椭圆
分别为椭圆![]() 的焦点,椭圆的右准线
的焦点,椭圆的右准线![]() 与
与![]() 轴交于
轴交于![]() 点,若
点,若![]() ,且
,且![]() .
.
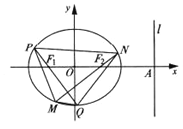
(Ⅰ)求椭圆的方程;
(Ⅱ)过![]() 、
、![]() 作互相垂直的两直线分别与椭圆交于
作互相垂直的两直线分别与椭圆交于![]() 、
、![]() 、
、![]() 、
、![]() 四点,求四边形
四点,求四边形![]() 面积的取值范围.
面积的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(I) 先确定A点坐标为(a2,0),利用![]() ,可得F2是AF1的中点,由此可求椭圆方程;(II)当直线MN与PQ中有一条与x轴垂直时,四边形PMQN面积
,可得F2是AF1的中点,由此可求椭圆方程;(II)当直线MN与PQ中有一条与x轴垂直时,四边形PMQN面积![]() ;当直线PQ,MN均与x轴不垂直时,设直线PQ、MN的方程与椭圆方程联立,求得|PQ|,|MN|,表示出四边形PMQN面积,再换元,即可求得四边形PMQN面积的取值范围.
;当直线PQ,MN均与x轴不垂直时,设直线PQ、MN的方程与椭圆方程联立,求得|PQ|,|MN|,表示出四边形PMQN面积,再换元,即可求得四边形PMQN面积的取值范围.
(Ⅰ)由![]() 得
得![]() ,∴
,∴![]() 点坐标为
点坐标为![]() ;∵
;∵![]() ∴
∴![]() 是
是![]() 的中点∴
的中点∴![]() ,
,![]() ∴椭圆方程为
∴椭圆方程为![]()
(Ⅱ)当直线![]() 与
与![]() 之一与
之一与![]() 轴垂直时,四边形
轴垂直时,四边形![]() 面积
面积![]() ;
;
当直线![]() ,
,![]() 均与
均与![]() 轴不垂直时,不妨设
轴不垂直时,不妨设![]() ,
,
联立 代入消去
代入消去![]() 得
得![]()
设![]() ,
,![]() 则
则![]() ,
,![]()
∴![]() ,同理
,同理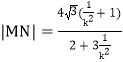
∴四边形![]() 面积
面积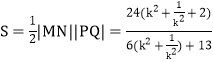
令![]() ,则
,则![]() ,
,![]() ,易知
,易知![]() 是以
是以![]() 为变量的增函数
为变量的增函数
所以当![]() ,
,![]() 时,
时,![]() ,∴
,∴![]()
综上可知,![]() ,∴四边形
,∴四边形![]() 面积的取值范围为
面积的取值范围为![]()

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目

