题目内容
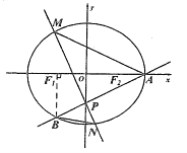
【题目】如果函数y=f(x)的导函数的图象如图所示,给出下列判断:
①函数y=f(x)在区间 ![]() 内单调递增;
内单调递增;
②函数y=f(x)在区间 ![]() 内单调递减;
内单调递减;
③函数y=f(x)在区间(4,5)内单调递增;
④当x=2时,函数y=f(x)有极小值;
⑤当x= ![]() 时,函数y=f(x)有极大值.
时,函数y=f(x)有极大值.
则上述判断中正确的是( )
A.①②
B.②③
C.③④⑤
D.③
【答案】D
【解析】对于①,函数y=f(x)在区间(﹣3,﹣ ![]() )内有增有减,故①不正确;
)内有增有减,故①不正确;
对于②,函数y=f(x)在区间(﹣ ![]() ,3)有增有减,故②不正确;
,3)有增有减,故②不正确;
对于③,函数y=f(x)当x∈(4,5)时,恒有f′(x)>0.故③正确;
对于④,当x=2时,函数y=f(x)有极大值,故④不正确;
对于⑤,当x=﹣ ![]() 时,f′(x)≠0,故⑤不正确.
时,f′(x)≠0,故⑤不正确.
故答案为:D.
利用使f′(x)>0的区间是增区间,使f′(x)<0的区间是减区间,分别对①②③进行逐一判定,导数等于零的值是极值,先增后减是极大值,先减后增是极小值,再对④⑤进行判定.导数和函数的单调性的关系:
(1)若f′(x)>0在(a,b)上恒成立,则f(x)在(a,b)上是增函数,f′(x)>0的解集与定义域的交集的对应区间为增区间;
(2)若f′(x)<0在(a,b)上恒成立,则f(x)在(a,b)上是减函数,f′(x)<0的解集与定义域的交集的对应区间为减区间.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目