题目内容
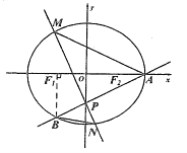
【题目】如图,椭圆 ![]() 的右顶点为
的右顶点为 ![]() ,左、右焦点分别为
,左、右焦点分别为 ![]() ,过点
,过点 ![]() 且斜率为
且斜率为 ![]() 的直线与
的直线与 ![]() 轴交于点
轴交于点 ![]() ,与椭圆交于另一个点
,与椭圆交于另一个点 ![]() ,且点
,且点 ![]() 在
在 ![]() 轴上的射影恰好为点
轴上的射影恰好为点 ![]() .
.
(1)求椭圆 ![]() 的标准方程;
的标准方程;
(2)过点 ![]() 的直线与椭圆交于
的直线与椭圆交于 ![]() 两点(
两点( ![]() 不与
不与 ![]() 重合),若
重合),若 ![]() ,求直线
,求直线 ![]() 的方程.
的方程.
【答案】
(1)解:当 ![]() 时,
时, ![]() 轴,得到点
轴,得到点 ![]()
所以
![]()
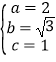 ,所以椭圆
,所以椭圆 ![]() 的方程是
的方程是 ![]()
(2)解:因为 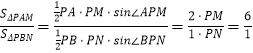 ,
, ![]() 所以
所以 ![]() .
.
设 ![]() ,则
,则 ![]() ,有
,有 ![]()
①当 ![]() 斜率不存在,
斜率不存在, ![]() 的方程为
的方程为 ![]() ,
,![]() 或
或 ![]() ,(不合条件,舍去)
,(不合条件,舍去)
②当 ![]() 斜率存在,由(Ⅰ)可知
斜率存在,由(Ⅰ)可知 ![]() ,设
,设 ![]() 方程为
方程为 ![]() ,
,
联立方程 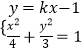 得:
得: ![]() .
.
由韦达定理可得 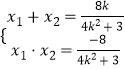 ,将
,将 ![]() 代入可得
代入可得 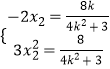 ,
,
即 ![]() .所以
.所以 ![]() .
.
所以直线 ![]() 的方程为
的方程为 ![]() 或
或 ![]()
【解析】(1)首先由条件得到直线AP的方程,根据“B和F1”的横坐标相同可得到B的坐标,代入直线AP,得到a,b,c一组关系;再由椭圆的性质a2=b2+c2得到一组关系;最后根据A点坐标,得到a=2,代入方程求解b,c的值。
(2)由上题已知A,B的坐标,面积之比为6,可以利用三角函数表示三角形的面积,将面积比转化为边长比,再转化为向量比,向量由点的坐标表示,可设出M,N的坐标和直线MN的方程;联立直线MN和椭圆,得到系数由k表示的一元二次方程,根据韦达定理得到x1和x2的关系,进而得到直线MN的斜率k。

练习册系列答案
相关题目