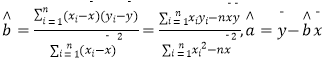题目内容
【题目】在空间中, ![]() 是两条不同的直线,
是两条不同的直线, ![]() 是两个不同的平面,则下列命题中的真命题是( )
是两个不同的平面,则下列命题中的真命题是( )
A.若 ![]() ,
, ![]() ,则
,则 ![]()
B.若 ![]() ,
, ![]() ,
, ![]() ,则
,则 ![]()
C.若 ![]() ,
, ![]() ,则
,则 ![]()
D.若 ![]() ,
, ![]() 则
则 ![]()
【答案】D
【解析】 ![]() 中,若
中,若 ![]() ,
, ![]() ,则
,则 ![]() ,则
,则 ![]() 与
与 ![]() 平行,相交或者异面,故不符合题意;
平行,相交或者异面,故不符合题意;
在 ![]() 中,若
中,若 ![]() ,
, ![]() ,
, ![]() ,则
,则 ![]() 与
与 ![]() 平行,相交或者异面,故不符合题意;
平行,相交或者异面,故不符合题意;
在 ![]() 中,若
中,若 ![]() ,
, ![]() ,则
,则 ![]() 或
或 ![]() 平面
平面 ![]() 内,故不符合题意;
内,故不符合题意;
在 ![]() 中,若
中,若 ![]() ,
, ![]() ,则由线面平行的判定定理得
,则由线面平行的判定定理得 ![]() ,故符合题意;
,故符合题意;
所以答案是: ![]()
【考点精析】本题主要考查了空间中直线与平面之间的位置关系的相关知识点,需要掌握直线在平面内—有无数个公共点;直线与平面相交—有且只有一个公共点;直线在平面平行—没有公共点才能正确解答此题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
【题目】(某保险公司有一款保险产品的历史户获益率(获益率=获益÷保费收入)的频率分布直方图如图所示: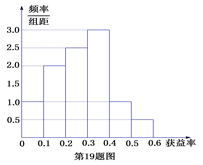
(Ⅰ)试估计平均收益率;
(Ⅱ)根据经验若每份保单的保费在 ![]() 元的基础上每增加
元的基础上每增加 ![]() 元,对应的销量
元,对应的销量 ![]() (万份)与
(万份)与 ![]() (元)有较强线性相关关系,从历史销售记录中抽样得到如下
(元)有较强线性相关关系,从历史销售记录中抽样得到如下 ![]() 组
组 ![]() 与
与 ![]() 的对应数据:
的对应数据:
|
|
|
|
|
|
销量 |
|
|
|
|
|
(ⅰ)根据数据计算出销量 ![]() (万份)与
(万份)与 ![]() (元)的回归方程为
(元)的回归方程为 ![]() ;
;
(ⅱ)若把回归方程 ![]() 当作
当作 ![]() 与
与 ![]() 的线性关系,用(Ⅰ)中求出的平均获益率估计此产品的获益率,每份保单的保费定为多少元时此产品可获得最大获益,并求出该最大获益.
的线性关系,用(Ⅰ)中求出的平均获益率估计此产品的获益率,每份保单的保费定为多少元时此产品可获得最大获益,并求出该最大获益.
参考公示: