题目内容
11.设函数f(x)=|2x-4|,g(x)=|x+1|.(1)解不等式:f(x)>g(x);
(2)当x∈[0,3],求函数y=f(x)+g(x)的最大值.
分析 (1)由题意,|2x-4|>|x+1|,两边平方,即可解不等式;
(2)当x∈[0,3],分类讨论,去掉绝对值符号,即可求函数y=f(x)+g(x)的最大值.
解答 解:(1)由题意,|2x-4|>|x+1|,
∴(2x-4)2>(x+1)2,…(1分)
∴(3x-3)(x-5)>0…(2分)
∴x<1或x>5,…(3分),
即不等式的解集为{x|x<1或x>5}.…(4分)
(2)x∈[0,3]时,x+1>0,y=|2x-4|+|x+1|=|2x-4|+x|+1…(5分)
当0≤x≤2时,y=4-2x+x+1=5-x在[0,2]上递减,…(6分),
故当x=0时,ymax=5…(7分)
当2<x≤3时,y=2x-4+x+1=3x-3在(2,3]上递增…(8分),
故当x=3时,ymax=6…(9分)
综上,当x=3时,y的最大值为6.…(10分)
点评 本题考查绝对值不等式,考查不等式的解法,考查函数的最大值,考查分类讨论的数学思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.随机变量ξ~B(100,0.3),则D(3ξ-5)等于( )
| A. | 62 | B. | 84 | C. | 184 | D. | 189 |
6.已知a=$\frac{\sqrt{5}}{2}$,函数f(x)=ax,若实数m,n满足f(m)>f(-n),则m,n满足的关系为( )
| A. | m+n<0 | B. | m+n>0 | C. | m>n | D. | m<n |
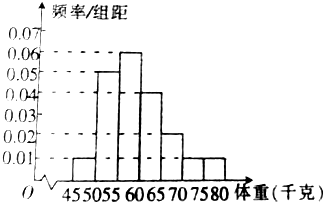
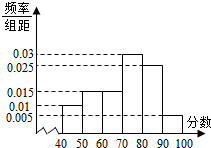 从参加环保竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示,观察图形,回答下列问题:
从参加环保竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示,观察图形,回答下列问题: