题目内容
【题目】如图所示，在正三棱柱ABCA1B1C1中，AB=2，AA1=2，由顶点B沿棱柱侧面(经过棱AA1)到达顶点C1，与AA1的交点记为M.求：
(1)三棱柱侧面展开图的对角线长；
(2)从B经M到C1的最短路线长及此时
的值.
【答案】(1) 
.
(2)
1.
【解析】
（1）正三棱柱ABC﹣A1B1C1的侧面展开图是长为6，宽为2的矩形，直接可以求出对角线长；
（2）将侧面AA1B1B绕棱AA1旋转120°使其与侧面AA1C1C在同一平面上，点B运动到点D的位置，连接DC1交AA1于M，则DC1就是由顶点B沿棱柱侧面经过棱AA1到顶点C1的最短路线，求出DC1和
的值即可；
沿侧棱BB1将正三棱柱的侧面展开，得到一个矩形BB1B′1B′(如下图).
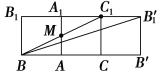
(1)矩形BB1B′1B′的长BB′=6，宽BB1=2.所以三棱柱侧面展开图的对角线长为
=2
.
(2) 如图，将侧面AA1B1B绕棱AA1旋转120°使其与侧面AA1C1C在同一平面上，点B运动到点D的位置，连接DC1交AA1于M，则DC1就是由顶点B沿棱柱侧面经过棱AA1到顶点C1的最短路线，其长为
∵△DMA≌△C1MA1，∴AM=A1M，故
练习册系列答案
相关题目
