ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΘ§«ζœΏΠΘ”…«ζœΏC1ΘΚ ![]() Θ®aΘΨbΘΨ0Θ§yΓή0Θ©ΚΆ«ζœΏC2ΘΚ
Θ®aΘΨbΘΨ0Θ§yΓή0Θ©ΚΆ«ζœΏC2ΘΚ ![]() Θ®aΘΨ0Θ§bΘΨ0Θ§yΘΨ0Θ©Ήι≥…Θ§Τδ÷–ΒψF1 Θ§ F2ΈΣ«ζœΏC1Υυ‘Ύ‘≤ΉΕ«ζœΏΒΡΫΙΒψΘ§ΒψF3 Θ§ F4ΈΣ«ζœΏC2Υυ‘Ύ‘≤ΉΕ«ζœΏΒΡΫΙΒψΘ§
Θ®aΘΨ0Θ§bΘΨ0Θ§yΘΨ0Θ©Ήι≥…Θ§Τδ÷–ΒψF1 Θ§ F2ΈΣ«ζœΏC1Υυ‘Ύ‘≤ΉΕ«ζœΏΒΡΫΙΒψΘ§ΒψF3 Θ§ F4ΈΣ«ζœΏC2Υυ‘Ύ‘≤ΉΕ«ζœΏΒΡΫΙΒψΘ§
Θ®ΔώΘ©»τF2Θ®2Θ§0Θ©Θ§F3Θ®©¹6Θ§0Θ©Θ§«σ«ζœΏΠΘΒΡΖΫ≥ΧΘΜ
Θ®ΔρΘ©»γΆΦΘ§Ής÷±œΏlΤΫ––”Ύ«ζœΏC2ΒΡΫΞΫϋœΏΘ§ΫΜ«ζœΏC1”ΎΒψAΓΔBΘ§«σ÷ΛΘΚœ“ABΒΡ÷–ΒψM±Ί‘Ύ«ζœΏC2ΒΡΝμ“ΜΧθΫΞΫϋœΏ…œΘΜ
Θ®ΔσΘ©Ε‘”ΎΘ®ΔώΘ©÷–ΒΡ«ζœΏΠΘΘ§»τ÷±œΏl1ΙΐΒψF4ΫΜ«ζœΏC1”ΎΒψCΓΔDΘ§«σΓςCDF1ΟφΜΐΒΡΉν¥σ÷ΒΘ°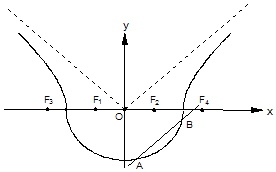
ΓΨ¥πΑΗΓΩΫβΘΚΘ®ΔώΘ©ΓΏF2Θ®2Θ§0Θ©Θ§F3Θ®©¹6Θ§0Θ©Θ§Γύ 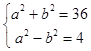 a
a 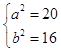 ‘ρ«ζœΏΠΘΒΡΖΫ≥ΧΈΣ
‘ρ«ζœΏΠΘΒΡΖΫ≥ΧΈΣ ![]() ΚΆ
ΚΆ ![]() Θ®yΘΨ0Θ©
Θ®yΘΨ0Θ©
Θ®ΔρΘ©«ζœΏC2ΒΡΫΞΫϋœΏΈΣy=Γά ![]() Θ§»γΆΦΘ§…η÷±œΏlΘΚy=
Θ§»γΆΦΘ§…η÷±œΏlΘΚy= ![]()
‘ρ 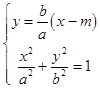 2x2©¹2mx+Θ®m2©¹a2Θ©=0
2x2©¹2mx+Θ®m2©¹a2Θ©=0
Γς=Θ®2mΘ©2©¹42Θ®m2©¹a2Θ©=8a2©¹4m2ΘΨ0©¹ ![]()
”÷”… ΐ–ΈΫαΚœ÷ΣmΓίaΘ§ ![]()
…ηΒψAΘ®x1 Θ§ y1Θ©Θ§BΘ®x2 Θ§ y2Θ©Θ§MΘ®x0 Θ§ y0Θ©‘ρ 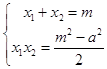 Θ§
Θ§
Γύ ![]() Θ§
Θ§ ![]()
Γύ ![]() Θ§Φ¥ΒψM‘Ύ÷±œΏy=©¹
Θ§Φ¥ΒψM‘Ύ÷±œΏy=©¹ ![]() …œΘ°
…œΘ°
Θ®ΔσΘ©”…Θ®ΔώΘ©÷ΣΘ§«ζœΏC1ΈΣ ![]() Θ§ΒψF4Θ®6Θ§0Θ©Θ°
Θ§ΒψF4Θ®6Θ§0Θ©Θ°
…η÷±œΏl1ΒΡΖΫ≥ΧΈΣx=ny+6Θ®nΘΨ0Θ©
”… 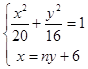 Θ®4n2+5Θ©y2+48ny+64=0
Θ®4n2+5Θ©y2+48ny+64=0
Γς=Θ®48nΘ©2©¹4ΓΝ64Θ®4n2+5Θ©ΘΨ0n2ΘΨ1
…ηCΘ®x3 Θ§ y3Θ©Θ§DΘ®x4 Θ§ y4Θ©”…ΈΛ¥οΕ®άμΘΚ 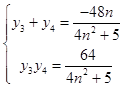
|y3©¹y4|= ![]() Θ°
Θ°
sΓςCDF1= ![]() |F1F4|ΓΝ|y3©¹y4|=
|F1F4|ΓΝ|y3©¹y4|= ![]()
Ννt= ![]() Θ§Γύn2=t2+1Θ§sΓςCDF1=64
Θ§Γύn2=t2+1Θ§sΓςCDF1=64 ![]() ΓΝ
ΓΝ 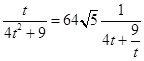
ΓΏtΘΨ0Θ§Γύ ![]() Θ§Β±«“ΫωΒ±t=
Θ§Β±«“ΫωΒ±t= ![]() Φ¥n=
Φ¥n= ![]() ±Β»Κ≈≥…ΝΔ
±Β»Κ≈≥…ΝΔ
Γύn= ![]() ±Θ§ΓςCDF1ΟφΜΐΒΡΉν¥σ÷Β
±Θ§ΓςCDF1ΟφΜΐΒΡΉν¥σ÷Β ![]()
ΓΨΫβΈωΓΩΘ®ΔώΘ©”…F2Θ®2Θ§0Θ©Θ§F3Θ®©¹6Θ§0Θ©Θ§Ω…ΒΟΘ© ![]() aΘ®ΔρΘ©«ζœΏC2ΒΡΫΞΫϋœΏΈΣΓά
aΘ®ΔρΘ©«ζœΏC2ΒΡΫΞΫϋœΏΈΣΓά ![]() Θ§»γΆΦΘ§…ηΒψAΘ®x1 Θ§ y1Θ©Θ§BΘ®x2 Θ§ y2Θ©Θ§MΘ®x0 Θ§ y0Θ©Θ§…η÷±œΏlΘΚy=
Θ§»γΆΦΘ§…ηΒψAΘ®x1 Θ§ y1Θ©Θ§BΘ®x2 Θ§ y2Θ©Θ§MΘ®x0 Θ§ y0Θ©Θ§…η÷±œΏlΘΚy= ![]() Θ§”κΆ÷‘≤ΖΫ≥ΧΝΣΝΔΜ·ΈΣ2x2©¹2mx+Θ®m2©¹a2Θ©=0Θ§άϊ”ΟΓςΘΨ0Θ§Ηυ”κœΒ ΐΒΡΙΊœΒΓΔ÷–ΒψΉχ±ξΙΪ ΫΘ§÷Μ“Σ÷ΛΟςy0=©¹
Θ§”κΆ÷‘≤ΖΫ≥ΧΝΣΝΔΜ·ΈΣ2x2©¹2mx+Θ®m2©¹a2Θ©=0Θ§άϊ”ΟΓςΘΨ0Θ§Ηυ”κœΒ ΐΒΡΙΊœΒΓΔ÷–ΒψΉχ±ξΙΪ ΫΘ§÷Μ“Σ÷ΛΟςy0=©¹ ![]() Φ¥Ω…Θ°Θ®ΔσΘ©…η÷±œΏl1ΒΡΖΫ≥ΧΈΣx=ny+6Θ®nΘΨ0Θ©Θ°”κΆ÷‘≤ΖΫ≥ΧΝΣΝΔΩ…ΒΟΘ®5+4n2Θ©y2+48ny+64=0Θ§άϊ”ΟΗυ”κœΒ ΐΒΡΙΊœΒΓΔœ“≥ΛΙΪ ΫΓΔ»ΐΫ«–ΈΒΡΟφΜΐΦΤΥψΙΪ ΫΓΔΜυ±Ψ≤ΜΒ» ΫΒΡ–‘÷ Φ¥Ω…ΒΟ≥ωΘ°
Φ¥Ω…Θ°Θ®ΔσΘ©…η÷±œΏl1ΒΡΖΫ≥ΧΈΣx=ny+6Θ®nΘΨ0Θ©Θ°”κΆ÷‘≤ΖΫ≥ΧΝΣΝΔΩ…ΒΟΘ®5+4n2Θ©y2+48ny+64=0Θ§άϊ”ΟΗυ”κœΒ ΐΒΡΙΊœΒΓΔœ“≥ΛΙΪ ΫΓΔ»ΐΫ«–ΈΒΡΟφΜΐΦΤΥψΙΪ ΫΓΔΜυ±Ψ≤ΜΒ» ΫΒΡ–‘÷ Φ¥Ω…ΒΟ≥ωΘ°

 Ωλά÷–Γ≤© ΩΙ°ΙΧ”κΧαΗΏœΒΝ–¥πΑΗ
Ωλά÷–Γ≤© ΩΙ°ΙΧ”κΧαΗΏœΒΝ–¥πΑΗΓΨΧβΡΩΓΩ![]() Ρξ
Ρξ![]() ‘¬
‘¬![]() »’Θ§ΓΑΙζΦ ΫΧ”ΐ–≈œΔΜ·¥σΜαΓ±‘Ύ…ΫΕΪ«ύΒΚΩΣΡΜ.ΈΣΝΥΫβΡΡ–©»ΥΗϋΙΊΉΔΓΑΙζΦ ΫΧ”ΐ–≈œΔΜ·¥σΜαΓ±Θ§Ρ≥ΜζΙΙΥφΜζ≥ι»ΓΝΥΡξΝδ‘Ύ
»’Θ§ΓΑΙζΦ ΫΧ”ΐ–≈œΔΜ·¥σΜαΓ±‘Ύ…ΫΕΪ«ύΒΚΩΣΡΜ.ΈΣΝΥΫβΡΡ–©»ΥΗϋΙΊΉΔΓΑΙζΦ ΫΧ”ΐ–≈œΔΜ·¥σΜαΓ±Θ§Ρ≥ΜζΙΙΥφΜζ≥ι»ΓΝΥΡξΝδ‘Ύ![]() -
-![]() Υξ÷°ΦδΒΡ
Υξ÷°ΦδΒΡ![]() »ΥΫχ––Βς≤ιΘ§≤ΔΑ¥ΡξΝδΜφ÷Τ≥…ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§»γΆΦΥυ ΨΘ§ΤδΖ÷Ήι«χΦδΈΣΘΚ
»ΥΫχ––Βς≤ιΘ§≤ΔΑ¥ΡξΝδΜφ÷Τ≥…ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§»γΆΦΥυ ΨΘ§ΤδΖ÷Ήι«χΦδΈΣΘΚ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() .Α―ΡξΝδ¬δ‘Ύ«χΦδ
.Α―ΡξΝδ¬δ‘Ύ«χΦδ![]() ΚΆ
ΚΆ![]() ΡΎΒΡ»ΥΖ÷±π≥ΤΈΣΓΑ«ύ…ΌΡξΓ±ΚΆΓΑ÷–άœΡξΓ±.
ΡΎΒΡ»ΥΖ÷±π≥ΤΈΣΓΑ«ύ…ΌΡξΓ±ΚΆΓΑ÷–άœΡξΓ±.

ΙΊΉΔ | ≤ΜΙΊΉΔ | ΚœΦΤ | |
«ύ…ΌΡξ |
| ||
÷–άœΡξ | |||
ΚœΦΤ |
|
|
|
Θ®1Θ©ΗυΨίΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ«σ―υ±ΨΒΡ÷–ΈΜ ΐΘ®±ΘΝτΝΫΈΜ–Γ ΐΘ©ΚΆ÷Ύ ΐΘΜ
Θ®2Θ©ΗυΨί“―÷ΣΧθΦΰΆξ≥…![]() Ν–ΝΣ±μΘ§≤Δ≈–ΕœΡήΖώ”–
Ν–ΝΣ±μΘ§≤Δ≈–ΕœΡήΖώ”–![]() ΒΡΑ―Έ’»œΈΣΓΑ÷–άœΡξΓ±±»ΓΑ«ύ…ΌΡξΓ±ΗϋΦ”ΙΊΉΔΓΑΙζΦ ΫΧ”ΐ–≈œΔΜ·¥σΜαΓ±ΘΜ
ΒΡΑ―Έ’»œΈΣΓΑ÷–άœΡξΓ±±»ΓΑ«ύ…ΌΡξΓ±ΗϋΦ”ΙΊΉΔΓΑΙζΦ ΫΧ”ΐ–≈œΔΜ·¥σΜαΓ±ΘΜ



