题目内容
(本小题14分)已知点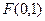 ,直线
,直线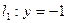 ,
,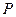 为平面上的动点,过点
为平面上的动点,过点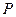 作直线
作直线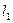 的垂线,垂足为点
的垂线,垂足为点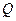 ,且
,且 .
.
(1)求动点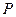 的轨迹
的轨迹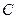 的方程;
的方程;
(2)轨迹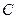 上是否存在一点
上是否存在一点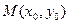 使得过
使得过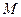 的切线
的切线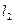 与直线
与直线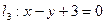 平行?若存在,求出
平行?若存在,求出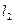 的方程,并求出它与
的方程,并求出它与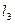 的距离;若不存在,请说明理由.
的距离;若不存在,请说明理由.
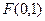 ,直线
,直线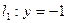 ,
,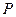 为平面上的动点,过点
为平面上的动点,过点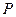 作直线
作直线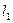 的垂线,垂足为点
的垂线,垂足为点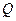 ,且
,且 .
.(1)求动点
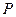 的轨迹
的轨迹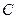 的方程;
的方程; (2)轨迹
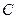 上是否存在一点
上是否存在一点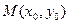 使得过
使得过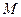 的切线
的切线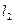 与直线
与直线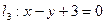 平行?若存在,求出
平行?若存在,求出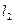 的方程,并求出它与
的方程,并求出它与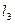 的距离;若不存在,请说明理由.
的距离;若不存在,请说明理由. 19.解:(1)设点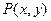 ,则
,则 ,
,
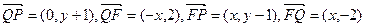
由 得
得 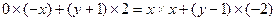
整理得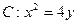 …………………5分
…………………5分
(2)假设轨迹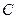 上存在一点
上存在一点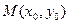 使得过
使得过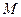 的切线
的切线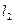 与直线
与直线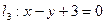 平行.
平行.
由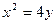 得
得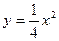 ,所以
,所以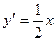 , …………………7分
, …………………7分
由假设可知,直线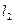 的斜率
的斜率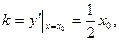 …………………8分
…………………8分
又直线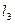 的斜率等于1,故
的斜率等于1,故 ,即
,即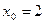 , …………………9分
, …………………9分
代入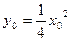 得
得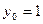 …………………10分
…………………10分
因此点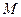 的坐标为
的坐标为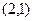 ,直线
,直线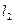 的方程为
的方程为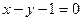 …………………12分
…………………12分
直线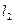 与直线
与直线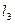 的距离
的距离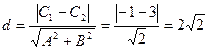 . …………………14分
. …………………14分
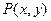 ,则
,则 ,
,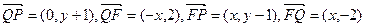
由
 得
得 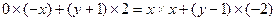
整理得
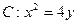 …………………5分
…………………5分(2)假设轨迹
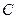 上存在一点
上存在一点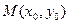 使得过
使得过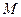 的切线
的切线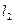 与直线
与直线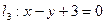 平行.
平行.由
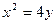 得
得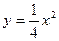 ,所以
,所以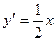 , …………………7分
, …………………7分由假设可知,直线
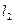 的斜率
的斜率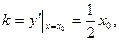 …………………8分
…………………8分又直线
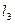 的斜率等于1,故
的斜率等于1,故 ,即
,即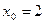 , …………………9分
, …………………9分代入
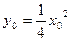 得
得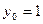 …………………10分
…………………10分因此点
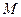 的坐标为
的坐标为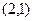 ,直线
,直线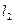 的方程为
的方程为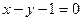 …………………12分
…………………12分直线
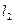 与直线
与直线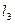 的距离
的距离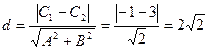 . …………………14分
. …………………14分略

练习册系列答案
相关题目
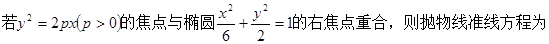 ( )
( )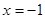
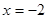
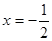
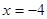
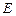 :
: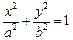 (
(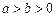 )过点
)过点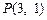 ,其左、右焦点分别为
,其左、右焦点分别为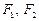 ,且
,且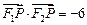 .
.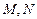 是直线
是直线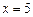 上的两个动点,且
上的两个动点,且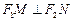 ,则以
,则以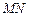 为直径的圆
为直径的圆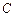 是否过定点?请说明理由.
是否过定点?请说明理由.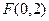 ,且与定直线
,且与定直线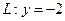 相切.
相切.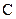 的方程;
的方程;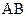 是轨迹
是轨迹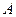 、
、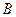 为切点作轨迹
为切点作轨迹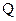 ,证明:
,证明: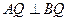 .
.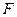 是椭圆
是椭圆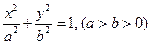 的左焦点,直线
的左焦点,直线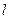 为对应的准线,直线
为对应的准线,直线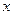 轴交于
轴交于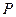 点,
点,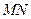 为椭圆的长轴,已知
为椭圆的长轴,已知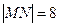 ,且
,且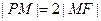 .
.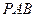 ,恒有
,恒有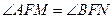 ;
;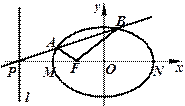
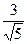 ,焦点坐标分别为F1(-2,0),F2(2,0),O是坐标原点.
,焦点坐标分别为F1(-2,0),F2(2,0),O是坐标原点.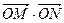 的值;
的值;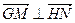 ,(s<k),分别以线段OG、OH为边作两个正方形,求这两上正方形的面积和的最小值,并求出取得最小值时G、H两点的坐标.
,(s<k),分别以线段OG、OH为边作两个正方形,求这两上正方形的面积和的最小值,并求出取得最小值时G、H两点的坐标.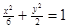 和双曲线
和双曲线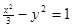 的公共点为
的公共点为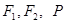 是两曲线的一个交点, 那么
是两曲线的一个交点, 那么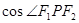 的值是
的值是
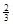
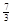
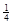
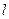 与抛物线
与抛物线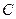 ,当直线
,当直线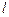 从
从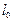 开始在平面上绕
开始在平面上绕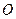 点按逆时针方向匀速旋转(旋转的角度不超过
点按逆时针方向匀速旋转(旋转的角度不超过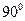 )时,它扫过的面积
)时,它扫过的面积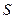 是时间
是时间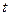 的函数,则函数图象大致是
的函数,则函数图象大致是
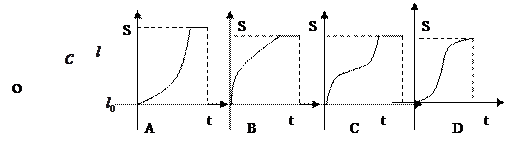
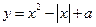 有两个交点,则
有两个交点,则 的取值范围是
的取值范围是