题目内容
【题目】成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列{bn}中的b3、b4、b5.
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)数列{bn}的前n项和为Sn,求证:数列{Sn+![]() }是等比数列.
}是等比数列.
【答案】(Ⅰ)![]() (Ⅱ)详见解析
(Ⅱ)详见解析
【解析】
试题分析:(I)利用成等差数列的三个正数的和等于15可设三个数分别为5-d,5,5+d,代入等比数列中可求d,进一步可求数列{bn}的通项公式;(II)根据(I)及等比数列的前 n项和公式可求![]() ,要证数列
,要证数列![]() 是等比数列
是等比数列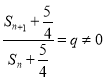 即可
即可
试题解析:(I)设成等差数列的三个正数分别为a﹣d,a,a+d
依题意,得a﹣d+a+a+d=15,解得a=5
所以{bn}中的依次为7﹣d,10,18+d
依题意,有(7﹣d)(18+d)=100,解得d=2或d=﹣13(舍去)
故{bn}的第3项为5,公比为2
由b3=b122,即5=4b1,解得![]()
所以{bn}是以![]() 首项,2为公比的等比数列,通项公式为
首项,2为公比的等比数列,通项公式为![]() ……………6分
……………6分
(II)数列{bn}的前和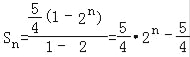
即![]() ,所以
,所以![]() ,
,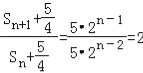
因此{![]() }是以
}是以![]() 为首项,公比为2的等比数列 …………………12分
为首项,公比为2的等比数列 …………………12分

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目