题目内容
【题目】已知圆![]() 经过点A(-2,0),B(0,2),且圆心
经过点A(-2,0),B(0,2),且圆心![]() 在直线y=x上,又直线l:y=kx+1与圆
在直线y=x上,又直线l:y=kx+1与圆![]() 相交于P、Q两点.
相交于P、Q两点.
(1)求圆![]() 的方程;
的方程;
(2)若![]() ,求实数k的值;
,求实数k的值;
(3)过点![]() 作动直线
作动直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点.试问:在以
两点.试问:在以![]() 为直径的所有圆中,是否存在这样的圆
为直径的所有圆中,是否存在这样的圆![]() ,使得圆
,使得圆![]() 经过点
经过点![]() ?若存在,求出圆
?若存在,求出圆![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在圆
;(3)存在圆![]() 或
或![]() ,使得圆
,使得圆![]() 经过点
经过点![]() .
.
【解析】
试题分析:(1)根据题意设出圆心![]() 和半径
和半径![]() ,列出
,列出![]() 和
和![]() 的方程,求得圆的方程;(2)根据
的方程,求得圆的方程;(2)根据![]() ,
,
求得![]() ,所以圆心到直线
,所以圆心到直线![]() 的距离为
的距离为![]() ,求得
,求得![]() 的值;(3)若圆
的值;(3)若圆![]() 经过点
经过点![]() ,则必有
,则必有![]() 即
即![]() ①,当直线
①,当直线![]() 的斜率不存在时,显然满足题意得圆,当直线
的斜率不存在时,显然满足题意得圆,当直线![]() 的斜率存在时,设其斜率为
的斜率存在时,设其斜率为![]() ,直线
,直线![]() 的方程为:
的方程为:![]() ,代入圆
,代入圆![]() 的方程,由韦达定理,得到
的方程,由韦达定理,得到![]() 的值,联立①解得
的值,联立①解得![]() 的值,存在所求的圆,进而得到所求的圆的方程.
的值,存在所求的圆,进而得到所求的圆的方程.
试题解析:(1)设圆心C(a,a),半径为r.因为圆C经过点A(-2,0),B(0,2),所以|AC|=|BC|=r,易得a=0,r=2,所以圆C的方程是![]() . 3分
. 3分
(2)因为![]() ·
·![]() =2×2×cos〈
=2×2×cos〈![]() ,
,![]() 〉=-2,且
〉=-2,且![]() 与
与![]() 的夹角为∠POQ,
的夹角为∠POQ,
所以cos∠POQ=-![]() ,∠POQ=120°,所以圆心C到直线l:kx-y+1=0的距离d=1,
,∠POQ=120°,所以圆心C到直线l:kx-y+1=0的距离d=1,
又d=![]() ,所以
,所以![]() . 7分
. 7分
(联立直线与圆的方程求解酌情给分)
(3)(ⅰ)当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 经过圆
经过圆![]() 的圆心
的圆心![]() ,此时直线
,此时直线![]() 与圆
与圆![]() 的交点为
的交点为![]() ,
,![]() ,
,![]() 即为圆
即为圆![]() 的直径,而点
的直径,而点![]() 在圆
在圆![]() 上,即圆
上,即圆![]() 也是满足题意的圆 8分
也是满足题意的圆 8分
(ⅱ)当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() ,由
,由![]() ,
,
消去![]() 整理,得
整理,得![]() ,由△
,由△![]() ,得
,得![]() 或
或![]() .
.
设![]() ,则有
,则有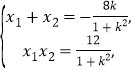 ① 9分
① 9分
由①得![]() , ②
, ②
![]() , ③
, ③
若存在以![]() 为直径的圆
为直径的圆![]() 经过点
经过点![]() ,则
,则![]() ,所以
,所以![]() ,
,
因此![]() ,即
,即![]() , 10分
, 10分
则![]() ,所以
,所以![]() ,
,![]() ,满足题意. 12分
,满足题意. 12分
此时以![]() 为直径的圆的方程为
为直径的圆的方程为![]() ,
,
即![]() ,亦即
,亦即![]() . 13分
. 13分
综上,在以![]() 为直径的所有圆中,存在圆
为直径的所有圆中,存在圆![]() :
:![]() 或
或
![]() ,使得圆
,使得圆![]() 经过点
经过点![]() . 14分
. 14分

【题目】为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间x(单位:小时)与当天投篮命中率y之间的关系:
时间x | 1 | 2 | 3 | 4 | 5 |
命中率y | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
小李这5天的平均投篮命中率为 ;用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率为 .






