题目内容
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,椭圆C和抛物线y2=x交于M,N两点,且直线MN恰好通过椭圆C的右焦点.
,椭圆C和抛物线y2=x交于M,N两点,且直线MN恰好通过椭圆C的右焦点.
(1)求椭圆C的标准方程;
(2)经过椭圆C右焦点的直线l和椭圆C交于A,B两点,点P在椭圆上,且 ![]() =2
=2 ![]() ,其中O为坐标原点,求直线l的斜率.
,其中O为坐标原点,求直线l的斜率.
【答案】
(1)解:由椭圆的离心率e= ![]() =
= ![]() ,a=
,a= ![]() c,
c,
由b2=a2﹣c2,则b=c,
设a=2λ,b=c= ![]() λ,λ>0,
λ,λ>0,
椭圆C和抛物线y2=x交于M,N两点,且直线MN恰好通过椭圆C的右焦点,
∴M(c, ![]() ),代入椭圆中得:
),代入椭圆中得: ![]() +
+ ![]() =1,即
=1,即 ![]() +
+ ![]() =1,解得:λ=
=1,解得:λ= ![]() ,∴a=2
,∴a=2 ![]() ,b=c=2,
,b=c=2,
故椭圆方程为: ![]()
(2)解:设A(x1,y1),B(x2,y2),P(x0,y0),则 ![]() =(x1,y1),
=(x1,y1), ![]() =(x0﹣x2,y0﹣y2),
=(x0﹣x2,y0﹣y2),
由 ![]() =2
=2 ![]() ,
,
∴(x1,y1)=2(x0﹣x2,y0﹣y2)
∴ 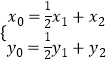 ,
,
由于A,B,P均在椭圆x2+2y2=8上,
∴ ![]() ①,
①, ![]() ②,
②, ![]() ③;
③;
由③可知: ![]() (
( ![]() )+(
)+( ![]() )+(x1x2+2y1y2)=8,
)+(x1x2+2y1y2)=8,
将第①②代入上式得:x1x2+2y1y2=﹣2,④
由直线l的斜率不为零,设直线l方为x=my+2,
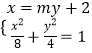 ,整理得:(m2+2)y2+4my﹣4=0,
,整理得:(m2+2)y2+4my﹣4=0,
由韦达定理y1+y2=﹣ ![]() ,y1y2=﹣
,y1y2=﹣ ![]() ,
,
将④变形为:(my1+2)(my2+2)+2y1y2=﹣2,
即(m2+2)y1y2+2m(y1+y2)+6=0,
∴2﹣ ![]() =0,解得:m2=
=0,解得:m2= ![]() ,m=±
,m=± ![]() ,
,
∵直线的斜率k= ![]() =±
=± ![]() ,
,
故直线l的斜率为± ![]()
【解析】(1)由题意可知:e= ![]() 知,即a=
知,即a= ![]() c,则b=c,设a=2λ,b=c=
c,则b=c,设a=2λ,b=c= ![]() λ,λ>0,将M(c,
λ,λ>0,将M(c, ![]() ),代入,即可求得λ的值,求得椭圆C的标准方程;(2)由题意可知则
),代入,即可求得λ的值,求得椭圆C的标准方程;(2)由题意可知则 ![]() =(x1 , y1),
=(x1 , y1), ![]() =(x0﹣x2 , y0﹣y2),
=(x0﹣x2 , y0﹣y2), ![]() =2
=2 ![]() ,即(x1 , y1)=2(x0﹣x2 , y0﹣y2),由于A,B,P均在椭圆x2+2y2=8上,则
,即(x1 , y1)=2(x0﹣x2 , y0﹣y2),由于A,B,P均在椭圆x2+2y2=8上,则 ![]() ,整理可得:x1x2+2y1y2=﹣2,设直线l方为x=my+2,代入椭圆方程,由韦达定理可知代入可知:2﹣
,整理可得:x1x2+2y1y2=﹣2,设直线l方为x=my+2,代入椭圆方程,由韦达定理可知代入可知:2﹣ ![]() =0,解得m的值,直线l的斜率为
=0,解得m的值,直线l的斜率为 ![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某城镇社区为了丰富辖区内广大居民的业余文化生活,创建了社区“文化丹青”大型活动场所,配备了各种文化娱乐活动所需要的设施,让广大居民健康生活、积极向上,社区最近四年内在“文化丹青”上的投资金额统计数据如表: (为了便于计算,把2015年简记为5,其余以此类推)
年份 | 5 | 6 | 7 | 8 |
投资金额 | 15 | 17 | 21 | 27 |
(Ⅰ)利用所给数据,求出投资金额![]() 与年份
与年份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(Ⅱ) 预测该社区在2019年在“文化丹青”上的投资金额.
附:对于一组数据![]() , 其回归直线
, 其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.