题目内容
【题目】已知函数
的导函数
只有一个极值点，在同一平面直角坐标系中，函数及的图象可以为（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】A,其中有一个拐点的图像是导函数的图像，另一个为原函数的图像，则当导函数的函数值为负时，原函数是单调递减的，导函数函数值为正时原函数单调递增，符合实际，故是正确的；
B其中有一个拐点的图像是导函数的图像，另一个为原函数的图像，当导函数的函数值为负时，原函数不是单调递减的，不符合题意，故不正确；
C其中有一个拐点的图像是导函数的图像，另一个为原函数的图像，在小于0的区间内，导函数为正，原函数应该是单调递增的，原图不符合这一条件，故不正确;
D其中有一个拐点的图像是导函数的图像，另一个为原函数的图像，整个导函数的图像都在x轴的上方，故原图应该是单调递增的，图像不符合这一实际，故不正确.
故答案为：A.
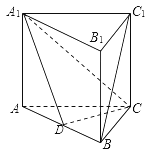
【题目】如图,四棱柱ABCD－A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD,
.
（1）证明: A1BD // 平面CD1B1;
（2）求三棱柱ABD－A1B1D1的体积.
【题目】某城镇社区为了丰富辖区内广大居民的业余文化生活，创建了社区“文化丹青”大型活动场所，配备了各种文化娱乐活动所需要的设施，让广大居民健康生活、积极向上，社区最近四年内在“文化丹青”上的投资金额统计数据如表: (为了便于计算，把2015年简记为5，其余以此类推)
年份 | 5 | 6 | 7 | 8 |
投资金额 | 15 | 17 | 21 | 27 |
(Ⅰ)利用所给数据，求出投资金额
与年份
之间的回归直线方程
；
(Ⅱ) 预测该社区在2019年在“文化丹青”上的投资金额.
附:对于一组数据
, 其回归直线的斜率和截距的最小二乘估计分别为
.
【题目】为了增强消防安全意识，某中学对全体学生做了一次消防知识讲座，从男生中随机抽取50人，从女生中随机抽取70人参加消防知识测试，统计数据得到如下列联表：
优秀 | 非优秀 | 总计 | |
男生 | 15 | 35 | 50 |
女生 | 30 | 40 | 70 |
总计 | 45 | 75 | 120 |
（Ⅰ）试判断是否有
的把握认为消防知识的测试成绩优秀与否与性别有关；
附：
K2=
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（Ⅱ）为了宣传消防安全知识，从该校测试成绩获得优秀的同学中采用分层抽样的方法，随机选出6名组成宣传小组，现从这6人中随机抽取2名到校外宣传，求到校外宣传的同学中至少有1名是男生的概率．
