题目内容
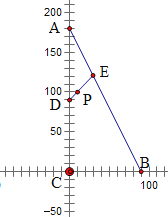
【题目】某小区有一块三角形空地，如图△ABC，其中AC=180米，BC=90米，∠C=90°，开发商计划在这片空地上进行绿化和修建运动场所，在△ABC内的P点处有一服务站（其大小可忽略不计），开发商打算在AC边上选一点D，然后过点P和点D画一分界线与边AB相交于点E，在△ADE区域内绿化，在四边形BCDE区域内修建运动场所. 现已知点P处的服务站与AC距离为10米，与BC距离为100米. 设
米，试问
取何值时，运动场所面积最大?
【答案】当
时，绿化面积最小，从而运动场所面积最大
【解析】
以C为坐标原点，CB所在直线为x轴，CA所在直线为y轴建立直角坐标系，得到C、A、B、P、D的坐标，再写出直线DE、AB的方程，由此联立解出E的坐标，进而表示△ADE的面积，由换元法简化面积表达式，从而利用基本不等式的知识分析可得答案.
以C为坐标原点，CB所在直线为x轴，CA所在直线为y轴建立直角坐标系，
则
，
，
，
，
.
DE所在直线方程为
，①
AB所在直线方程为
，②
解①、②组成的方程组得，
，
直线DE经过点B时
，
，
则
，
设
，
，
(当且仅当
时取等号)，
此时
，
当时，绿化面积最小，从而运动场所面积最大.
练习册系列答案
相关题目
